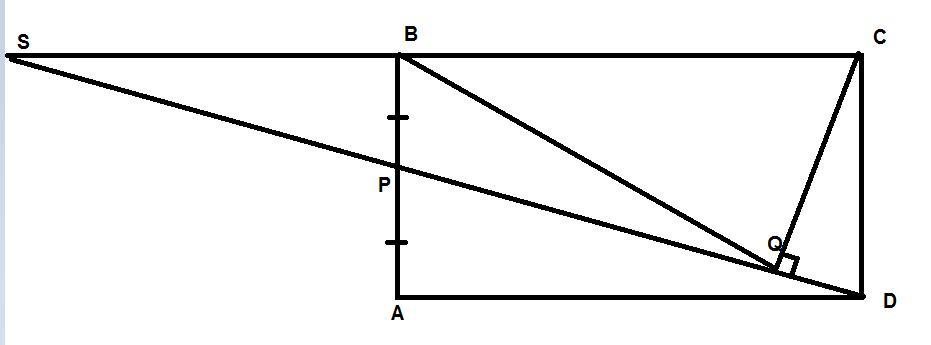
У прямокутнику ABCD точка P - середина сторони AB, а точка Q - основа перпендикуляра, опущеного з вершини C на PD. Докажіть, що BQ = BC.
Ответы на вопрос
Ответил hderyb
2
Пошаговое объяснение:
Продлим PQ до пересечения с BC, пусть точка пересечения будет S. В таком случае SB=AD из равенства треугольников SBP и APD по стороне и двум прилежащим углам. Т.к. AD=BC, то SB=BC => BQ-медиана из прямого угла, а значит BQ=SB=BC ч.т.д
Приложения:
ГАЗ52:
Клёво.
Не то слово , ништяк в квадрате
Ответил antonovm
2
Ответ:
Ещё одно решение :
Пошаговое объяснение:
Приложения:

можно без синусов , равные дуги стягиваются равными хордами , если получится исправлю
Подкалываете?!
не , выражаю СТЕПЕНЬ восхищения
Новые вопросы
Литература,
11 месяцев назад
Українська мова,
11 месяцев назад
Музыка,
1 год назад
Химия,
1 год назад
Английский язык,
6 лет назад