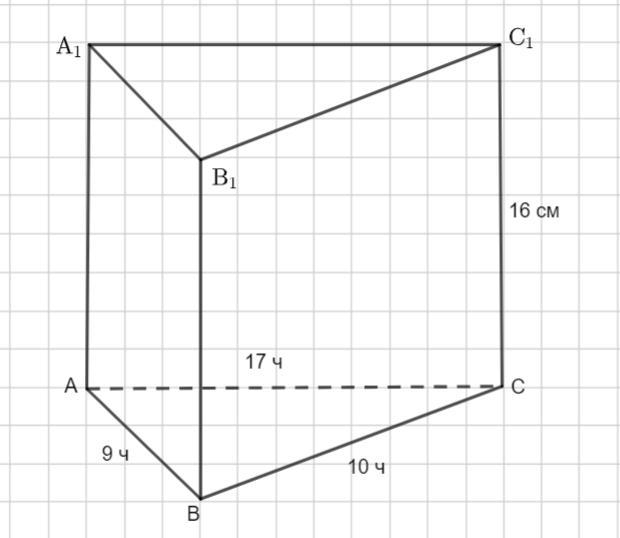
Математика, вопрос задал zverevvlades6 , 2 года назад

У прямій трикутній призмі сторони основи відносяться, як 17 : 10 : 9, а бічне ребро дорівнює 16 см. Повна поверхня цієї призми дорівнює 1440 $см^{2}$ . Знайдіть її бічну поверхню. ( у см $x^{2}$ )

НМТ 2022

Ответы на вопрос

Ответил lilyatomach

Ответ:

Площадь боковой поверхности призмы равна 1152 см²

Пошаговое объяснение:

В прямой треугольной призме стороны основания относятся,

как 17 : 10 : 9, а боковое ребро равно 16 см. Площадь полной поверхности призмы равна 1440 см². Найти площадь боковой поверхности призмы.

Пусть дана прямая призма $ABCA_{1} B_{1} C_{1}$ . Боковое ребро $AA_{1} =16$ см.

Стороны основания АС: ВС : АВ = 17 : 10 : 9.

Пусть одна часть будет х см. Тогда стороны основания АС =17х см,

ВС =10х см, АВ = 9х см.

Площадь полной поверхности равна

Sполн. = S бок. +2Sосн.

Площадь боковой поверхности призмы равна произведению периметра основания на боковое ребро .

Периметр треугольника - это сумма длин всех сторон.

Р осн. = АВ+ВС+АС

Росн. =9х +10х + 17х=36х см.

Тогда площадь боковой поверхности будет равна

$S =36x \cdot 16$ см².

Найдем площадь основания , то есть площадь треугольника по формуле Герона

$S =\sqrt{p(p-a)(p-b)(p-c)} ,$

где $p=\dfrac{a+b+c}{2}$ , a,b,c - стороны треугольника.

$p= \dfrac{36x}{2} =18x$

$S=\sqrt{18x(18x-17x)(18x-10x)(18x-9x)} =\sqrt{18x\cdot x\cdot 8x\cdot 9x} =\\\\=\sqrt{9x\cdot x\cdot16x\cdot9x} =9x\cdot 4x =36x^{2}$

Так как по условию площадь полной поверхности призмы равна 1440 см², то составляем уравнение

$2\cdot 36x^{2} + 36x\cdot16 =1440|:36 ;\\2x^{2} +16x-40=0|:2\\x^{2} +8x-20=0;\\D=8^{2} -4\cdot1\cdot(-20) = 64+80=144=12^{2} ;\\\\x{_1}= \dfrac{-8-12}{2} =-\dfrac{20}{2} =-10;\\\\x{_2}= \dfrac{-8+12}{2} =\dfrac{4}{2} =2$

Условию задачи удовлетворяет х=2.

Найдем площадь боковой поверхности призмы

$S =36\cdot2\cdot 16=36\cdot32=1152$ cм²

Значит, площадь боковой поверхности призмы равна 1152 см²

#SPJ1

Приложения:

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Українська мова, 1 год назад

Допоможіть будь ласка потрібно навести приклади трьох слів, утворених префіксальним способом Заранее дякую...

Русский язык, 1 год назад

Какой род у слова сказать...

Алгебра, 2 года назад

100 баллов! срочно! решить уравнение! с подробным пошаговым решением $\sqrt{x - 7} + \sqrt[3]{x} = 3$ ...

Математика, 2 года назад

Різниця між першим і другим числами дорівнює 4.перше число збільшили на 15 а друге на 13.як змінилася різниця?

Физика, 7 лет назад

7. У ході лабораторної роботи учень рівномірно тягне по столу дерев’яний брусок, діючи на нього з горизонтальною силою 1,2 Н. Визначте коефіцієнт тертя ковзання бруска по столу, якщо маса бруска...

География, 7 лет назад

Назовите и покажите по карте наиболее значимые природные объекты на территории США. СРОЧНОООО!!!!