У паралелограма АВСD висота BE ділить сторону AD на відрізки
AE = 8 см і ED = 20 см. Знайти діагональ ВD паралелограма, якщо його сторона АВ дорівнює 17 см. ДОПОМОЖІТЬ БУДЬ-ЛАСКА
Приложения:
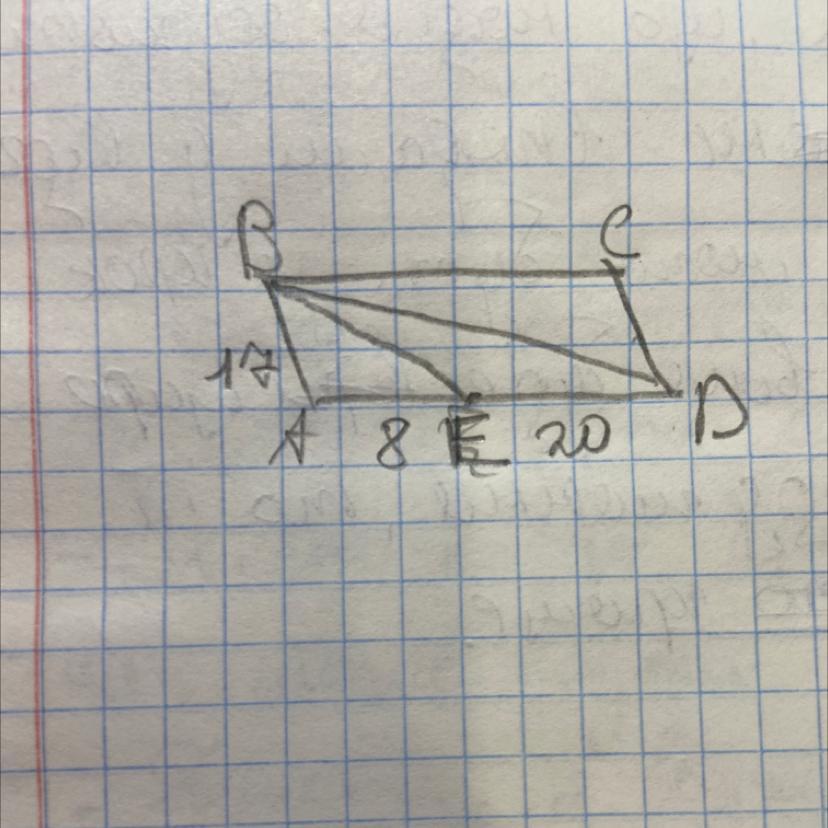
Ответы на вопрос
Ответил ReMiDa
2
Ответ:
Діагональ BD паралелограма ABCD дорівнює 25 см
Объяснение:
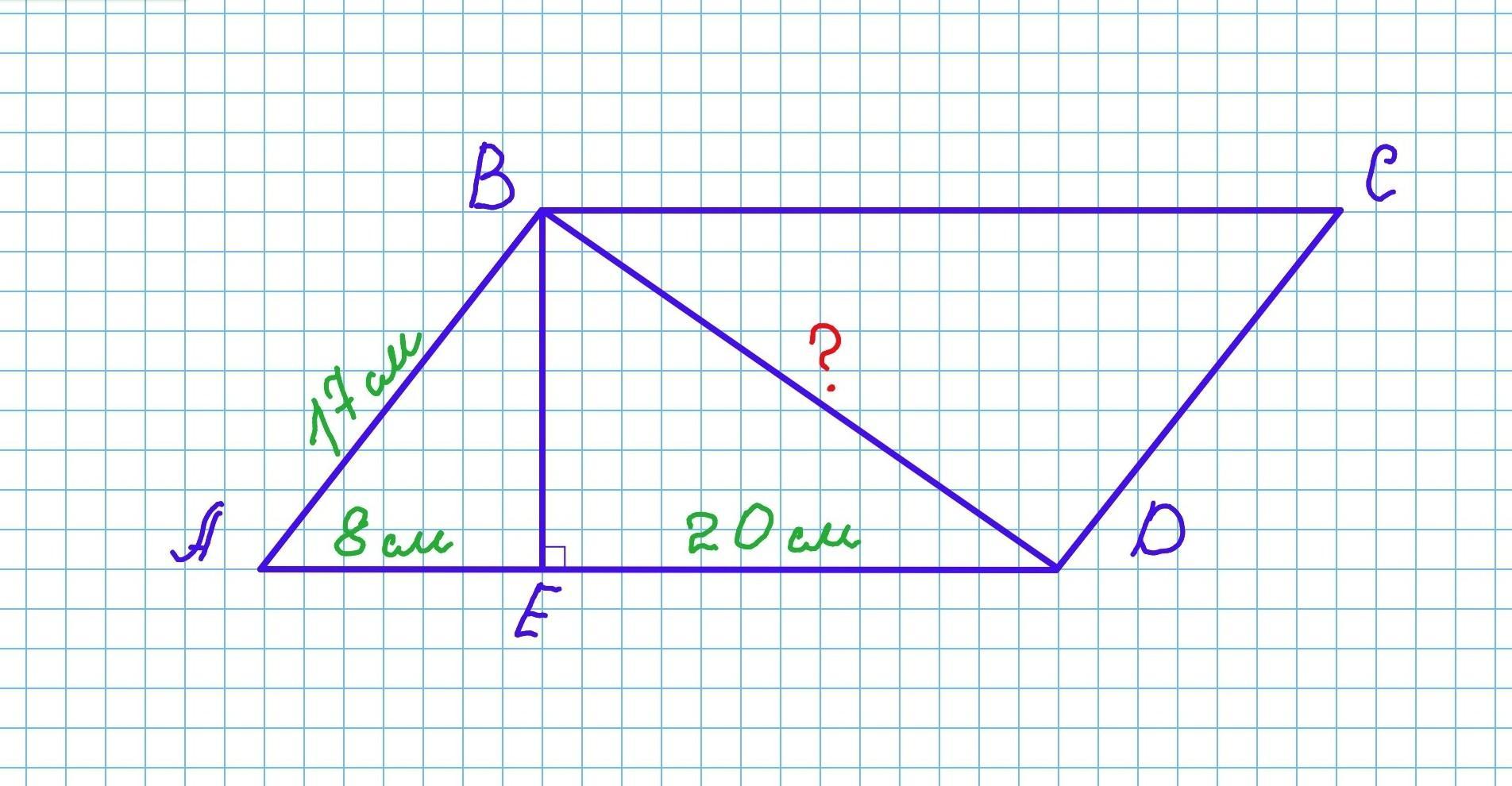
Пусть АВСD - параллелограмм, ВЕ - высота, проведенная к стороне AD. ВЕ⟂AD. AE = 8 см, ED = 20 см, AB = 17 см.
Найдём диагональ BD параллелограмма АВСD.
Рассмотрим прямоугольный треугольник АВЕ (∠АВЕ=90°, т.к. ВЕ⟂AD).
По теореме Пифагора: АЕ²+ВЕ²=АВ², тогда ВЕ²=АВ²-АЕ²=17²-8²=289-64=225
Рассмотрим прямоугольный треугольник ВЕD (∠BED=90°).
По теореме Пифагора найдём катет BD:
BD²=BE²+ED²=225+20²=225+400=625
BD= 25 см
Диагональ параллелограмма равна 25 см.
Приложения:
Новые вопросы
Русский язык,
1 год назад
Русский язык,
1 год назад
Математика,
6 лет назад
Биология,
6 лет назад
Математика,
8 лет назад