У кулю, радіус якої дорівнює 7 см, вписано циліндр, висота якого дорівнює діаметру його основи. Знайти площу бічної поверхні циліндра.

Ответ:

28π см²

Объяснение:

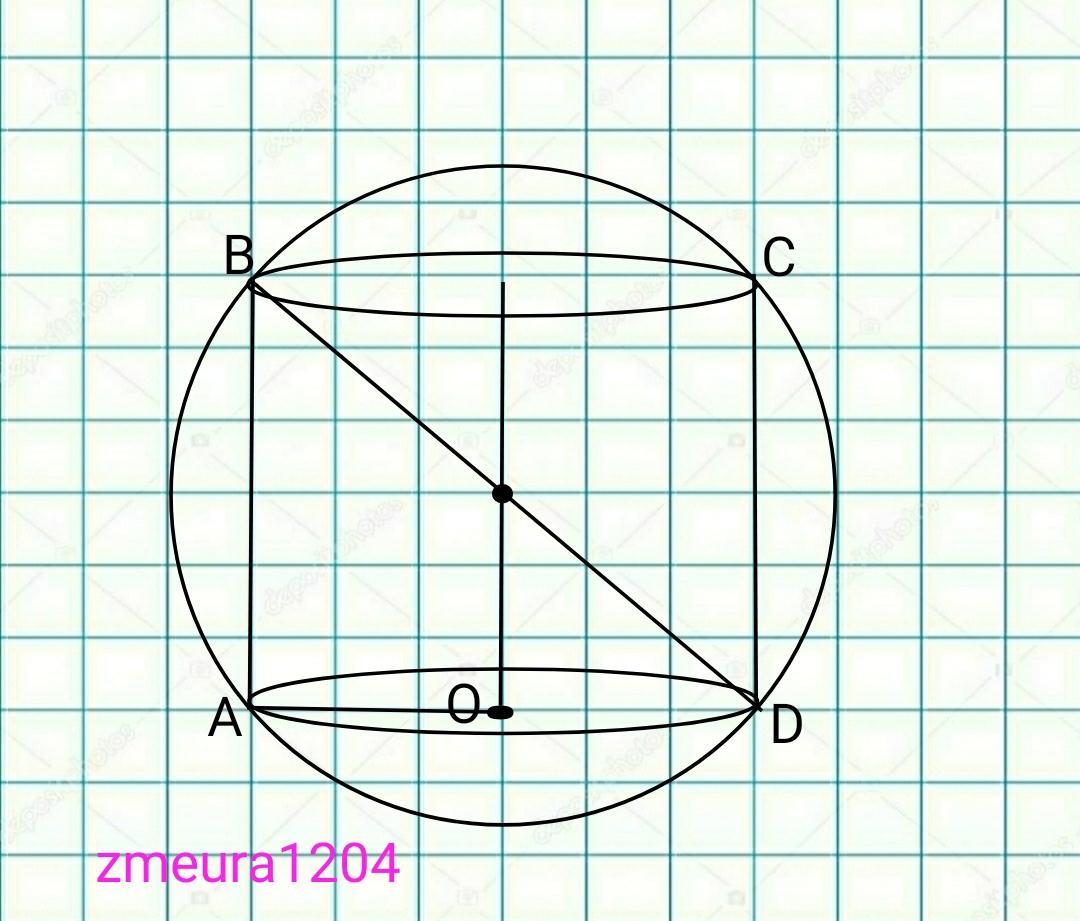
BD=2*7=14см диаметр шара и диагональ осевого сечения цилиндра.

∆АВD- равнобедренный прямоугольный треугольник.

АВ=ВD/√2=14/√2=7√2см

AB=AD=7√2см

АО=АD/2=7√2/2=3,5√2 см радиус цилиндра

С=2*π*АО=2*π*3,5√2=7√2π см длина окружности основания цилиндра.

Sбок=С*АВ=7√2π*7√2=28π см²