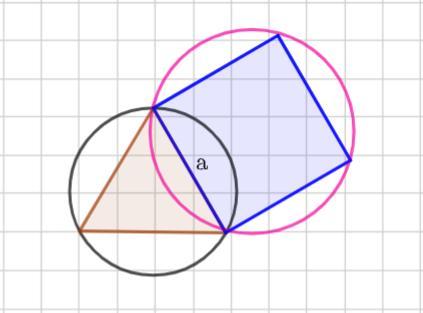
У коло, радіус якого дорівнює R, вписано правильний трикутник, а на його стороні побудовано квадрат. Знайдіть радіус кола, описаного навколо квадрата.

Ответ:

Объяснение:

В круг, радиус которого равен R вписан правильный треугольник , а на его стороне построен квадрат . Найти радиус круга, описанного около квадрата.

Пусть дан правильный треугольник со стороной а. Около этого правильного треугольника описан круг радиуса R .

Радиус окружности, описанной около правильного треугольника определяется по формуле

   где  a- сторона правильного треугольника.

Тогда найдем сторону этого треугольника

На стороне этого правильного треугольника построен квадрат.

Тогда сторона квадрата равна стороне правильного треугольника и равна

Около квадрата описана окружность. Радиус окружности, описанной около квадрата можно найти по формуле

 где а -сторона квадрата.

Тогда получим

-   радиус окружности, описанной около квадрата.

#SPJ1