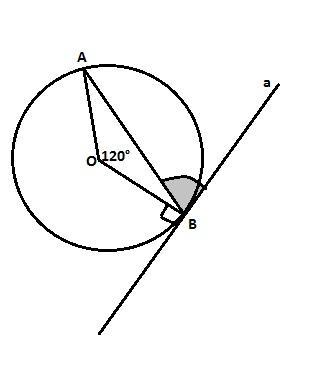
У колі з центром О проведено хорду АВ, причому кут АОВ = 120 градусів.
Знайдіть кут між хордою і дотичною проведеною до кола в точці В.
якщо можете + малюнок
Ответы на вопрос
Ответил ivanproh1
0
Угол между хордой и касательной равен половине градусной меры дуги, стягиваемой этой хордой (свойство), то есть половине градусной меры дуги АВ.
На дугу АВ опирается центральный угол АОБ, значит дуга АВ = 120°. Значит угол между касательной и хордой в точке касания равен 120°:2 = 60°
Ответ: искомый угол равен 60°.
Или так:
В равнобедренном треугольнике АОВ (стороны ОА и ОВ равны - радиусы) углы при основании равны по (180-120):2=30° (сумма углов треугольника = 180°). Касательная в точке касания перпендикулярна радиусу, значит искомый угол равен 90° - 30° = 60°.
Ответ: 60°
Приложения:
Новые вопросы
Английский язык,
1 год назад
Математика,
7 лет назад