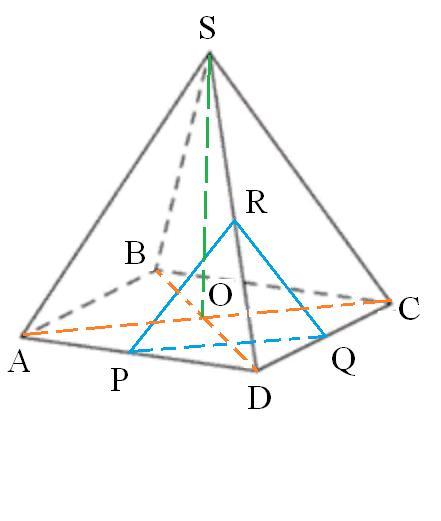
У чотирикутній піраміді SABCD проведено переріз площиною, яка проходить через точки P, Q і R — середини ребер AD, CD і SD відповідно. Знайдіть площу утвореного перерізу, якщо AB = BC = CD = AD = 4√2 см, SA = SB = SC = SD = 6 см
Ответы на вопрос
Ответил guvanch021272
3
Ответ:
2√5
Объяснение:
В силу условия данная пирамида правильная. Но всё же приведём док-во этого.
Проведём высоту пирамиды SO.
∠AOS=∠BOS=∠COS=∠AOS=90°, SA = SB = SC = SD, SO-общая⇒
⇒ΔAOS=ΔBOS=ΔCOS=ΔAOS⇒AO=BO=CO=DO
AB=BC=CD=AD, AO=BO=CO=DO⇒ABCD-квадрат
По теореме Пифагора
AC²=AB²+BC²=(4√2)²+(4√2)²=64⇒AC=8
P, Q и R — середины ребер AD, CD и SD⇒PQ, QR, PR-средние линии соответственно в ΔACD, ΔCSD, ΔASD
PQ=0,5AC=4
QR=0,5CS=3
PR=0,5AS=3
Найдём площадь ΔPRQ по теореме Герона.
p-полупериметр ΔPRQ
p=0,5(PQ+QR+PR)=0,5(3+3+4)=5
S²(ΔPRQ)=p(p-PQ)(p-PR)(p-QR)=5(5-3)(5-3)(5-4)=20
S(ΔPRQ)=√20=2√5
Приложения:
Новые вопросы
Математика,
1 год назад
Қазақ тiлi,
6 лет назад
Математика,
6 лет назад
Математика,
8 лет назад
Алгебра,
8 лет назад