Алгебра, вопрос задал Ulan96 , 9 лет назад

тригонометрия тендеу
3+5sin2x=cos4x

Ответы на вопрос

Ответил Аноним
0

В правой части уравнения применим формулу косинуса двойного угла

3+5sin 2x=1-2sin^22x\ \ 2sin^22x+5sin 2x+2=0

Решаем как квадратное уравнение относительно sin2x

D=5^2-4cdot 2cdot 2=9;~~~sqrt{D}=3

sin 2x=dfrac{-5-3}{2cdot 2}<-1 - уравнение решений не имеет.

sin 2x=dfrac{-5+3}{2cdot 2}=-dfrac{1}{2}\ \ 2x=(-1)^{k+1}cdot dfrac{pi}{6}+pi k,k in mathbb{Z}\ \ boldsymbol{x=(-1)^{k+1}cdot dfrac{pi}{12}+dfrac{pi k}{2},k in mathbb{Z}}

Ответил lilyatomach
0

Ответ:

решение представлено на фото

Объяснение:

Приложения:
Предыдущий вопрос
Следующий вопрос
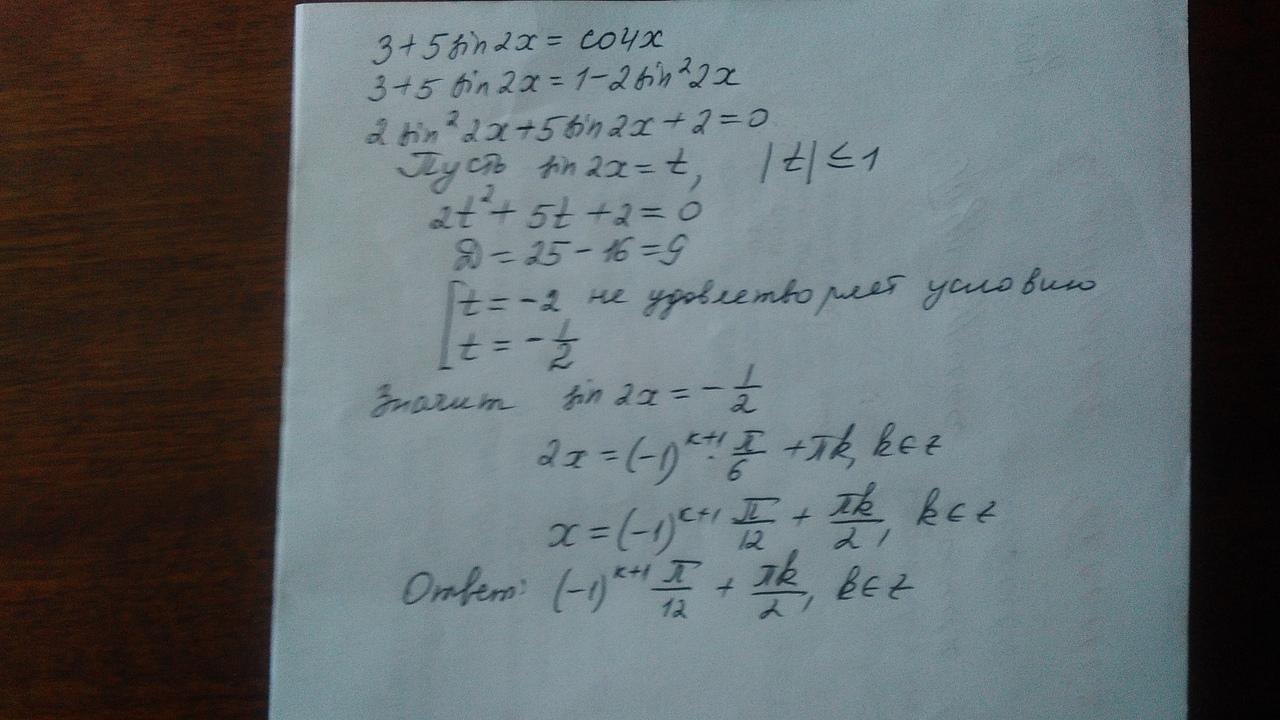
Новые вопросы
Английский язык, 2 года назад
Прочитайте текст и вставьте вместо каждого пропуска нужную грамматическую форму, выбрав её из выпадающего списка. A School for Geniuses? Theodore Tally is thirteen. He is from London. He A____...
Биология, 2 года назад
каковы функции рецепторов внутренних органов? СРОЧНО!!!​
Обществознание, 9 лет назад
пожалуйста скажите какой аргумент можно привести по эссе: право есть внешняя свобда человека,поределяемая общим законом...
Геометрия, 9 лет назад
Основания равнобедренной трапеции равны 23 и 17. Тангенс одного из углов равен −3/8 Найдите площадь трапеции.                                                                                   ...
Литература, 9 лет назад
назовите любую книгу о дружбе ,объясните  почему...
География, 9 лет назад
Природные зоны природная зона тундра (какие почвы),(растительность),(животные) природная зона тайга (какие почвы) (растительность) (животные) природная зона лесостепь (какие почвы) (растительность)...