Тригонометрия. Решить уравнение.
Приложения:
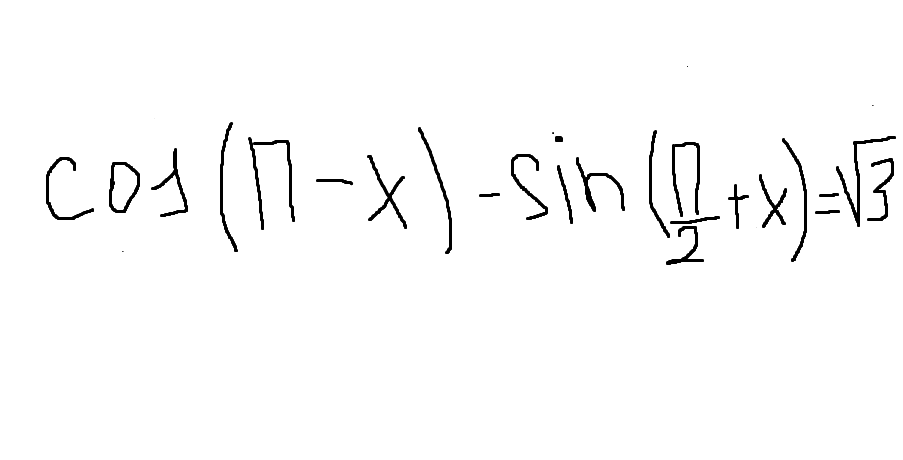
Ответы на вопрос
Ответил Аноним
0
cos(π-x) - sin(π/2 + x) = √3
-cos x-cosx = √3
cosx = -√3/2
x = ±5π/6 + 2πn,n ∈ Z
-cos x-cosx = √3
cosx = -√3/2
x = ±5π/6 + 2πn,n ∈ Z
Ответил antonbomba
0
Раскрываем скобки по правилам приведения. Первая скобка значение не меняет, тк Пи, косинус будет отриц. Вторая скобка значение менят на син, он будет положительный.
-cosx-cosx=корень из 3
-2cosx=корень из 3
cosx=-корень из 3/2
x=+-5Пи/6+2ПиN, N принадлежит Z
-cosx-cosx=корень из 3
-2cosx=корень из 3
cosx=-корень из 3/2
x=+-5Пи/6+2ПиN, N принадлежит Z
Новые вопросы