Алгебра, вопрос задал kksyusha03 , 2 года назад

Тригонометрия. Нужна помощь))

Приложения:

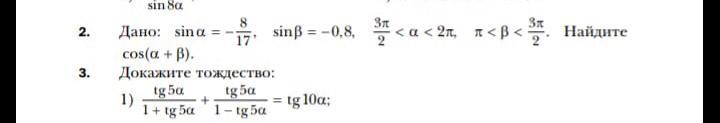
Ответы на вопрос

Ответил Universalka

1

1) α - угол четвёртой степени ⇒ Cosα > 0

β - угол третьей четверти ⇒ Cosβ < 0

$Cos\alpha=\sqrt{1-Sin^{2}\alpha} =\sqrt{1-(-\frac{8}{17})^{2}}=\sqrt{1-\frac{64}{289}} =\sqrt{\frac{225}{289}}=\frac{15}{17}\\\\Cos\beta =-\sqrt{1-Sin^{2}\beta } =-\sqrt{1-(-0,8)^{2}}=-\sqrt{1-0,64} =-\sqrt{0,36}=-0,6\\\\Cos(\alpha+\beta)= Cos\alpha Cos\beta-Sin\alpha Sin\beta=\frac{15}{17}*(-0,6)-(-\frac{8}{17})*(-0,8) =\\\\=-\frac{9}{17}-\frac{6,4}{17}=-\frac{15,4}{17}=-\frac{154}{170}=-\frac{77}{85}$

$2)\frac{tg5\alpha }{1+tg5\alpha }+\frac{tg5\alpha }{1-tg5\alpha }= \frac{tg5\alpha(1-tg5\alpha)+tg5\alpha(1+tg5\alpha)}{(1+tg5\alpha)(1-tg5\alpha)}=\\\\=\frac{tg5\alpha-tg^{2}5\alpha+tg5\alpha+tg^{2}5\alpha}{1-tg^{2}5\alpha}=\frac{2tg5\alpha}{1-tg^{2} 5\alpha}=tg10\alpha\\\\tg10\alpha =tg10\alpha$

Что и требовалсь доказать

kksyusha03: Спасибо тебе большое!

Universalka: Пожалуйста

instadiava: Помогите и мне пожалуйста у меня на стр

zvagi: здравствуй помогите мне пожалуста вопрос в профиле

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Русский язык, 1 год назад

Среди предложений 8-17 найдите сложное предложение с последовательным подчинением придаточных.Запишите номер этого предложения. Я думаю,что это 8,9,12! Но я неуверенна! И надо только одно...

Українська мова, 1 год назад

допоможіть скласти речення зі славосполученнями : мешкаю за адресою,змагання з футбоу,відсутній через хворобу,за всіма правилами , за нашими підрахунками. Тільки будьласка гарні речення...

Математика, 2 года назад

Запишите словосочетания «разность двух чисел», «сумма трёх чисел», «произведение пяти чисел», «Пять шестых числа», «в девять раз больше числа», «обратное числа» в виде буквенных выражений,...

Английский язык, 2 года назад

Пацани помогите нужно здать до восьми даю 30 балов!

Математика, 7 лет назад

Решите пожалуйста!! Если можно с подробным решением!!!

Физика, 7 лет назад

Какая приставка в названии физической величины означает её сотую долю? А) Деци В)Санти С)Милли Д)Микро Е)Мега...