Тригонометрическое уравнение под буквой а
Приложения:
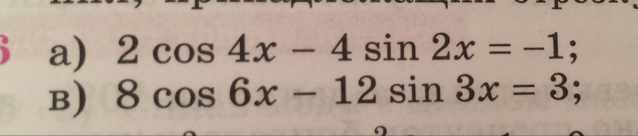
Ответы на вопрос
Ответил wolfstarrkk
0
2cos4x-sin2x=-1
2(cos²2x-sin²2x) - sin2x=-1
2cos²2x-2sin²2x-sin2x=-1
2(1-sin²2x)-2sin²2x-sin2x=-1
2-2sin²2x-2sin²2x-sin2x=-1
-4sin²2x-sin2x+3=0 |*(-1)
4sin²2x+sin2x-3=0
sin2x=a
4a²+a-3=0
D=(1)²-4*4*(-3)=1+48=49 ;
=7
a₁,₂=
= 
; -1
sin2x=
2x=(-1)ⁿ *arcsin() + Пn |:2
x=(-1)ⁿ *
arcsin () + Пn, n ∈Z
sin2x=-1
2x=-
+ 2
n |:2
x=-
∈Z
Ответ: x=(-1)ⁿ * arcsin () + Пn, n ∈Z ; x=-∈Z
2(cos²2x-sin²2x) - sin2x=-1
2cos²2x-2sin²2x-sin2x=-1
2(1-sin²2x)-2sin²2x-sin2x=-1
2-2sin²2x-2sin²2x-sin2x=-1
-4sin²2x-sin2x+3=0 |*(-1)
4sin²2x+sin2x-3=0
sin2x=a
4a²+a-3=0
D=(1)²-4*4*(-3)=1+48=49 ;
a₁,₂=
sin2x=
2x=(-1)ⁿ *arcsin(
x=(-1)ⁿ *
sin2x=-1
2x=-
x=-
Ответ: x=(-1)ⁿ *
Новые вопросы