Три сторони описаної трапеції, взяті послідовно, від­но­сяться, як 2:7:12. Знайдіть сторони трапеції, якщо її пе­ри­метр дорівнює 56 см.

Ответ: 4 см, 14 см, 24 см, 14 см.

Объяснение:

    Трапецию около окружности можно описать тогда и только тогда, когда сумма  длин её оснований равна сумме  длин боковых сторон.

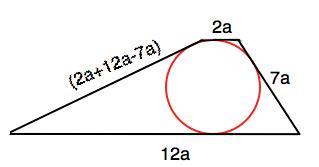
   Примем коэффициент отношений сторон трапеции равным а. Тогда основания равны 2а и 12а, а одна боковая сторона – 7а ( см. рисунок приложенного файла).

    Сумма длин оснований 2а+12а=14а, поэтому вторая боковая сторона 14а-7а=7а.

По условию Р=56 см =>

14а+14а=56 =>

а=56:28=2 (см)

Основания трапеции 2•2=4 (см); 2•7=14 (см) ; 2•12=24 (см); 2•7=14 (см).