Три луча выходят из одной точки и образуют три угла, каждый из которых меньше развёрнутого. Величина одного из них равна 100 градусов. Найдите угол между биссектрисами двух других углов.

Ответ:

130°

Объяснение:

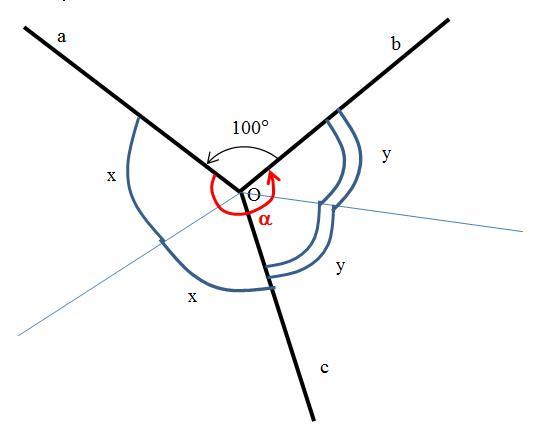
На рисунке три луча a, b и c выходят из точки О и образуют три угла. Величина одного из них равна 100 градусов. Так как полный угол равен 360°, то α = 360° - 100° = 260°.

Биссектриса делить угол на равные углы. Тогда если обозначит угол между биссектрисой и стороной угла через х, то угол между биссектрисой и другой стороной угла будет равен х. Далее, обозначим через у угол между биссектрисой и стороной второго угла, то угол между биссектрисой и другой стороной второго угла будет равен у.

С другой стороны α = x+x+y+y = 2·(x+y). Тогда

2·(x+y) = 260° ⇔ x+y = 130°.

Но угол x+y и есть угол между биссектрисами двух других углов.