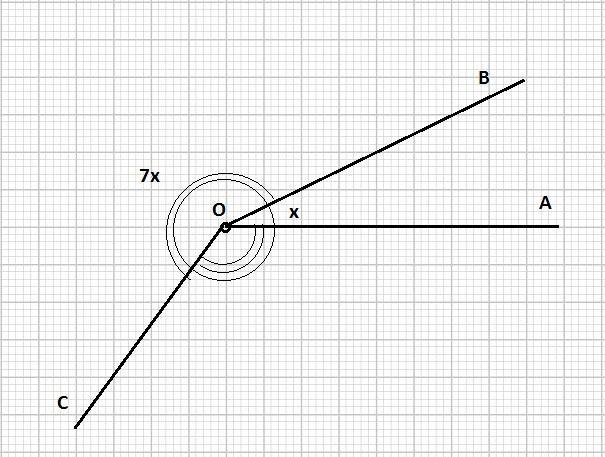
Три луча выходящие из одной точки разбивают плоскость на 3 различных по величине угла. Каждый угол измеряется целым числом градусов. Наубольший угол в 7 раз больше наименьшего. Сколько значений может принимать величина среднего угла. ТОЛЬКО С ОБЪЯСНЕНИЕМ!

Пусть ∠ AOB=x; ∠ AOC=3x; ∠ BOC=y

По условию

х+3х+у=360 ° ⇒ 4х = 360 ° – у⇒

х=90 ° –(у/4)

Так как по условию

x < y < 3x, то

90 ° – (y/4) < y < 270 ° – (3y/4)

Cистема

{90 ° – (y/4) < y ⇒ 5y/4 > 90 ° ⇒ y > 72 °

{y < 270 ° – (3y/4) ⇒ 7у/4 < 270 ° ⇒ у < 154 целых 2/7 °

72 ° < y < 154 целых 2/7 °

y= 73; 74; 75; ...; 154

Из них кратны четырем:

76; 80; 84; 88; ... ; 144; 148; 152.

b1=76

bn=152

bn=b1+4·(n–1)

152=76+4·(n–1)

n–1=76:4

n=20

О т в е т. 20

Ответ:

Объяснение:

Сделаем чертеж.

Пусть наименьший угол равен x.

Тогда наибольший угол равен 7x.

1)

Пусть средний угол равен наименьшему.

Составим уравнение:

x+7x+x = 360°

9x = 360°

x = 40°

Поскольку углы выражены целыми числами, а наименьший должен быть меньше среднего, то x<40;  x=39°

2)

Пусть средний угол равен наибольшему.

Составим уравнение:

x+7x+7x = 360°

15x = 360°

x = 24°

Поскольку углы выражены целыми числами, а наибольший  должен быть больше среднего, то x>24;  x=25°

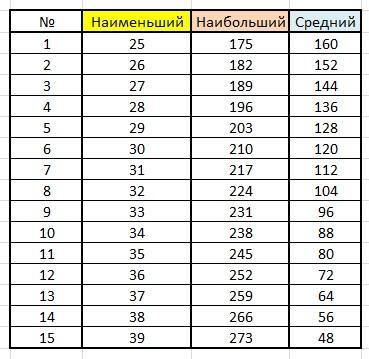
Итак, величина среднего угла лежит в интервале [25°; 39°].

Таких целых чисел 15. (смотри таблицу)