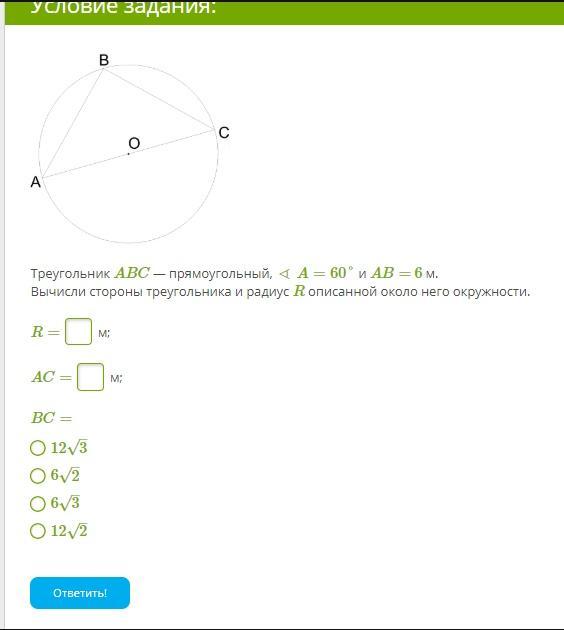
Треугольник ABC — прямоугольный, ∢ A=60° и AB= 6 м.
Вычисли стороны треугольника и радиус R описанной около него окружности.

Ответ: R= 6 м, АС = 12 м, ВС = 6 м

Объяснение:

Сумма острых углов прямоугольного  треугольника равна 90 градусов, поэтому угол С = 30°. Против угла 30° лежит катет равный половине гипотенузы, поэтому гипотенуза АС = 2*АВ = 2*6 = 12 м.

По теореме Пифагора, м

Тогда ВС = м

Гипотенуза этого треугольника является диаметром описанной окружности, поэтому R= = 6 м