Требуется выполнить задание из вложения
Приложения:
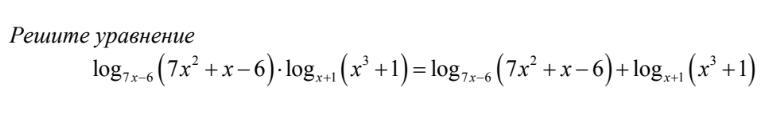
Ответы на вопрос
Ответил 25hjoerf10
0
Ответ:
х₁ = 7; х₂ = 1.
Объяснение:
Ответил 25hjoerf10
0
Ответы есть?
Ответил 25hjoerf10
0
Надеюсь, что решила правильно
Ответил ulivola
0
x=1 не является решением, т.к. в первый логарифм получается с основанием 1 по 2, всё остальное верно. Ответ: 7
Спасибо большое!
Спасибо большое!
Новые вопросы
Русский язык,
1 год назад
Українська мова,
1 год назад
Математика,
7 лет назад
Математика,
7 лет назад
Литература,
8 лет назад