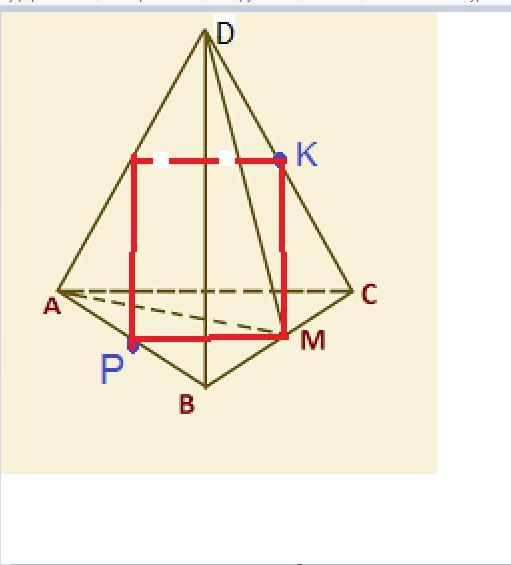
Точки P и K — середины ребер AB и DC правильной треугольной пирамиды DABC, все ребра которой равны. Постройте сечение пирамиды плоскостью, проходящей через данные точки и параллельной прямой AC. Определите периметр полученного сечения, если известно, что площадь полной поверхности пирамиды DABC равна
см2 .​

Получаем, что  в сечении каждая грань пересекается по средней линии.

Площадь одной грани как равностороннего треугольника равна a²√3/4. Умножаем на 4 грани и получаем, что Sп = 4*(a²√3/4) = a²√3.

Приравниваем площадь пирамиды заданному значению

a²√3 = 36√3, отсюда получаем а = √36 = 6.

Значит, длина стороны сечения равна 6/2 = 3.

Периметр Р = 4*3 = 12.

Ответ: Р = 12.