Точки M,H и P - параллельные проекции точек A B и D на плоскости альфа причем точка D принадлежит отрезку AB. Найдите AB если MH = 12 см НР = 8 см а BD = 14 см
Ответы на вопрос
Ответил mathkot
0
Ответ:
AB = 35
Объяснение:
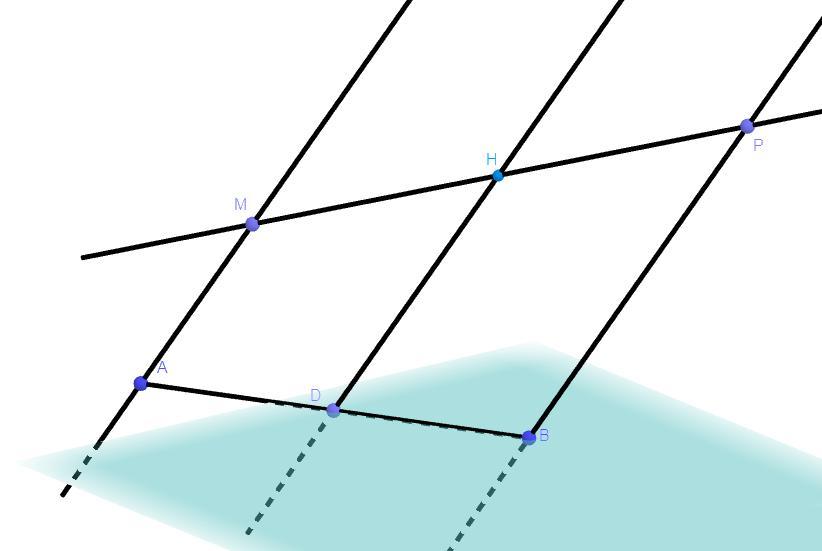
Дано: AM ║DH ║BP, A,B,D ∈ α, D ∈ AB, MH = 12, HP = 8, BD = 14
Найти: AB - ?
Решение: Через прямые AM, DH, BP можно провести одну и ту же плоскость и только одну по теореме, тогда плоскость проведенная через параллельный прямые AM, DH, BP пересекает плоскость по прямой по следствию из аксиом стереометрии. То ест точки A, D, B - лежат на одной прямой и в одной плоскости α (A,B,D ∈ α по условию).Так как по условию AM ║DH и DH ║BP то MADH и BDHP - трапеции по определению, так же эти трапеции лежат на параллельны прямых которые пересекают плоскость α в точках которые лежат на одной прямой тогда по теореме MADH и BDHP - подобные трапеции, следовательно ⇒
.
AB = AD + DB = 14 + 21 = 35.
Приложения:
Новые вопросы