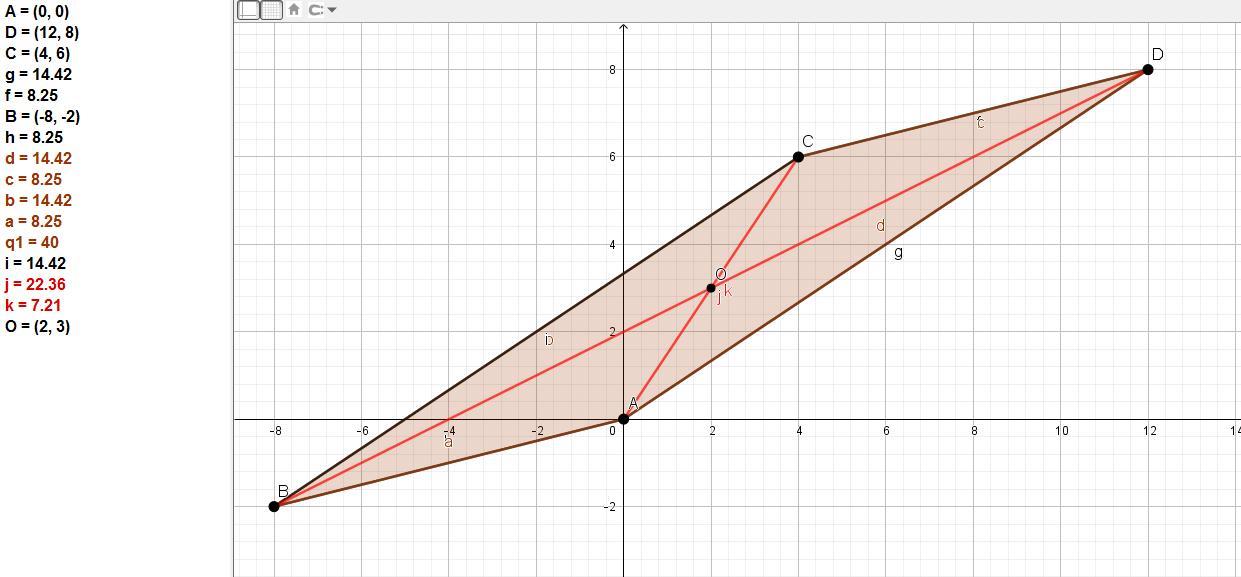
Точки A(0;0), Д(12;8), С(4;6) и В являются вершинами параллелограмма АБСД. Найдите координаты вершины В и точки пересечения диагонали ​

Свойство диагоналей параллелограмма: диагонали точкой персечения делятся пополам.

Поэтому:

АС и ВD - диагонали, О - точка их пересечения, т.е  О - середина  как АС, так и ВD.

Координаты середины отрезка равны полусумме соответствующих координат концов отрезка, значит, координаты точки О как середины отрезка АС будут таковы:

х₀ = (0 + 4)/2 = 2, у₀ = (0 + 6)/2 = 3.

Теперь найдем координаты точки В (х; у), т.к. О - середина также и отрезка ВD:

2 = (12 + х)/2, 12 + х = 4, откуда х = -8,

3 = (8 + у)/2, 8 + у = 6, откуда у = -2.

Ответ: В(-8; - 2).

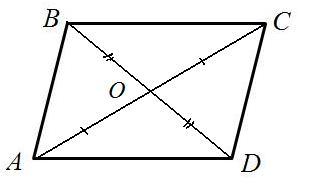
Можно эту задачу решать с помощью векторов.

Вектор ДС = (4-12; 6-8) = (-8; -2).

Координаты точки В равны: т.В = т.А + ДС.

Так как координаты точки А равны нулю, то точка В(-8; -2).

Точка пересечения диагоналей - это середина любой диагонали.

Проще взять АС. Точка О = (4/2; 6/2) = (2; 3).