Точка M, N и P лежат соответственно на сторонах AB, BC и CA треугольника ABC, причём MN параллельны AC, NP параллельны AB. Найдите стороны четырёхугольника AMNP, если а) AB=10см, AC=15см, PN:MN=2:3; б) AM=AP, AB=a, AC=B
Ответы на вопрос
Ответил KuOV
0
MN║AC, PN║AB, значит AMNP - параллелограмм, противоположные стороны равны.
MN║AC, ВС - секущая, тогда ∠BNM = ∠BCA как соответственные,
∠В - общий для ΔMBN и ΔАВС, значит
ΔMBN подобен ΔАВС по двум углам, ⇒
MN : AC = MB : AB
а)
Если х - коэффициент пропорциональности, то
PN = 2x, MN = 3x.
3x : 15 = (10 - 2x) : 10
30x = 150 - 30x
60x = 150
x = 2,5
PN = AM = 2 · 2,5 = 5 см,
MN = AP = 3 · 2,5 = 7,5 см
б)
Так как AMNP - параллелограмм, и его смежные стороны равны, то все стороны равны.
Пусть х - сторона AMNP.
Из подобия треугольников ΔMBN и ΔАВС:
MN : AC = MB : AB
x : b = (a - x) : a
ax = ab - bx
ax + bx = ab
x(a + b) = ab
x = ab / (a + b)
PN = AM = MN = AP = ab / (a+ b)
MN║AC, ВС - секущая, тогда ∠BNM = ∠BCA как соответственные,
∠В - общий для ΔMBN и ΔАВС, значит
ΔMBN подобен ΔАВС по двум углам, ⇒
MN : AC = MB : AB
а)
Если х - коэффициент пропорциональности, то
PN = 2x, MN = 3x.
3x : 15 = (10 - 2x) : 10
30x = 150 - 30x
60x = 150
x = 2,5
PN = AM = 2 · 2,5 = 5 см,
MN = AP = 3 · 2,5 = 7,5 см
б)
Так как AMNP - параллелограмм, и его смежные стороны равны, то все стороны равны.
Пусть х - сторона AMNP.
Из подобия треугольников ΔMBN и ΔАВС:
MN : AC = MB : AB
x : b = (a - x) : a
ax = ab - bx
ax + bx = ab
x(a + b) = ab
x = ab / (a + b)
PN = AM = MN = AP = ab / (a+ b)
Приложения:
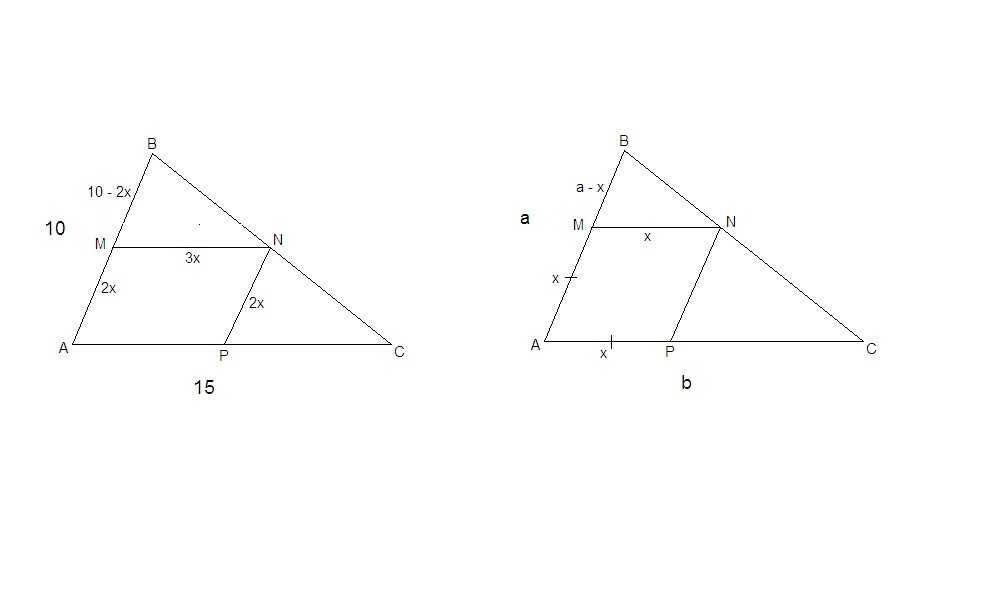
Новые вопросы