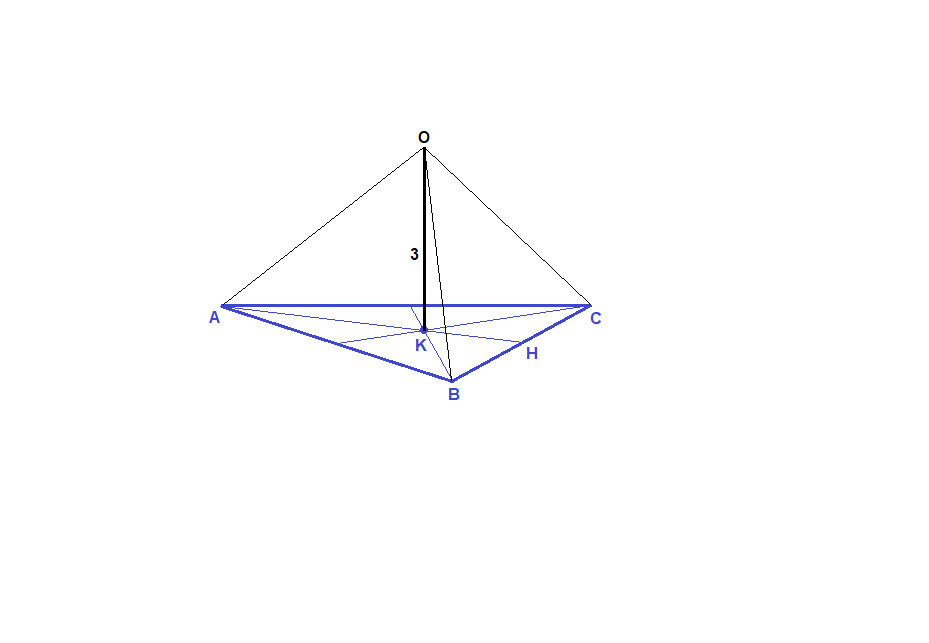
Точка К - точка пересечения высот равностороннего треугольника, длина высоты которая равна 6 см. Отрезок ОК перпендикулярен плоскости треугольника. Вычислите расстояние от точки О до вершин треугольника, если ОК = 3 см.

ΔABC равносторонний, поэтому высоты, медианы и биссектрисы в нем совпадают.

Медианы точкой пересечения делятся в отношении 2 : 1, считая от вершины. Значит

АК = ВК = СК = 2/3 АН = 2/3 · 6 = 4 см

ΔОАК = ΔОВК = ΔОСК по двум катетам, значит

ОА = ОВ = ОС.

ΔОАК: ∠ОКА = 90°, по теореме Пифагора

            ОА = √(ОК² + АК²) = √(9 + 16) = 5 см

ОА = ОВ = ОС = 5 см