Точка D на стороне AB треугольника ABC выбрана так, что AD=AC. Известно, что ∠CAB=10∘ и ∠ACB=166∘. Найдите угол DCB. Ответ дайте в градусах.
Ответы на вопрос
Ответил Аноним
0
Рассмотрим равнобедренный треугольник ADC.
Углы при основании равнобедренного треугольника равны.
∠ACD = (180 - 10) / 2 = 85∘
166 - 85 = 81∘
Ответ: 81∘
Углы при основании равнобедренного треугольника равны.
∠ACD = (180 - 10) / 2 = 85∘
166 - 85 = 81∘
Ответ: 81∘
Ответил monkeyme
0
Точно не уверен, но попробую.
Дано: тр-к ABC, т. D делит AB так, что AD = AC, <CAB = 10°, <ACB = 166°
Найти: <DCB - ?
Решение: Т.к. AD = AC, то тр-к ADC - равнобедр. (т.к. 2 стороны равны) → <ADC = <ACD (т.к. углы при основании равнобедр. треугольника равны). <CAD = 10° → 180 - 10 = 170° (это сумма углов <ADC и <ACD) → <ADC (<ACD) = 170 / 2 = 85°
Т.к. весь <ACB = 166, а нам надо узнать маленький кусочек <DCB → <DCB = 166 - 85 = 81°
Ответ: <DCB = 81°
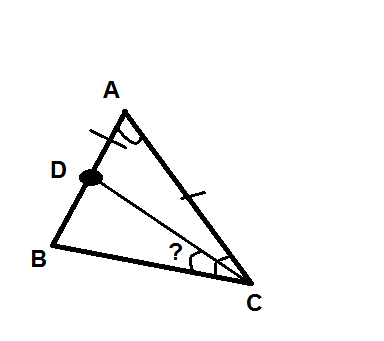
Рисунок не очень правильный... но какой смог..
Дано: тр-к ABC, т. D делит AB так, что AD = AC, <CAB = 10°, <ACB = 166°
Найти: <DCB - ?
Решение: Т.к. AD = AC, то тр-к ADC - равнобедр. (т.к. 2 стороны равны) → <ADC = <ACD (т.к. углы при основании равнобедр. треугольника равны). <CAD = 10° → 180 - 10 = 170° (это сумма углов <ADC и <ACD) → <ADC (<ACD) = 170 / 2 = 85°
Т.к. весь <ACB = 166, а нам надо узнать маленький кусочек <DCB → <DCB = 166 - 85 = 81°
Ответ: <DCB = 81°
Рисунок не очень правильный... но какой смог..
Приложения:
Новые вопросы