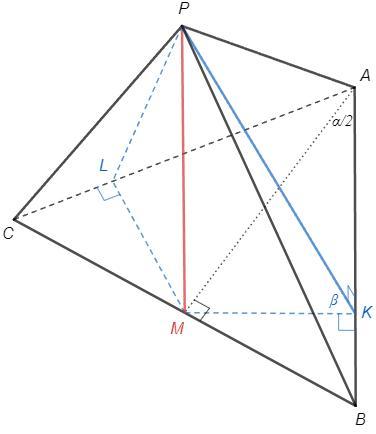
Геометрия, вопрос задал yanenefor , 11 месяцев назад

ТЕРМІНОВО!!!Основою піраміди є рівнобедрений трикутник з основою а і кутом £ при вершині. Бічна грань, що містить основу
цього трикутника, перпендикулярна до
основи, а дві інші - нахилені до неї під кутом В. Визначте бічну поверхню піраміди.

siestarjoki: Основанием пирамиды является равнобедренный треугольник с основанием а и углом при вершине альфа. Одна боковая грань перпендикулярна плоскости основания, а две другие наклонены к плоскости основания под углом бета. Найдите площадь боковой поверхности пирамиды.

Ответы на вопрос

Ответил siestarjoki

Ответ:

$\frac{a^2}{4} (cos\frac{\alpha}{2} tg\beta + \frac{ctg\frac{\alpha}{2}}{cos\beta})$

Объяснение:

Грань PBC, перпендикулярная основанию, содержит высоту пирамиды PM - точка М на BC.

Опустим перпендикуляр MK на AB. По теореме о трех перпендикулярах PK также перпендикуляр к AB. Угол между плоскостями - угол между перпендикулярами к общей прямой. ∠PKM - угол между боковой гранью PAB и основанием, ∠PKM=β.

Аналогично построим ∠PLM=β. Треугольники PKM и PLM равны по катету и острому углу. Точка M равноудалена от сторон угла BAC, следовательно лежит на его биссектрисе. △BAC -р/б, AM - биссектриса/высота/медиана.

MB =a/2

sinB =cos(BAM) =cos(α/2)

MK =MB sinB =a/2 *cos(α/2)

PM =MK tgβ =a/2 *cos(α/2) tgβ

S(PBC) =1/2 BC*PM =a^2/4 *cos(α/2) tgβ

AB =MB/sin(α/2) =a/2 *1/sin(α/2)

PK =MK/cosβ =a/2 *cos(α/2)/cosβ

S(PAB) =1/2 AB*PK =1/2 *a^2/4 *ctg(α/2)/cosβ

PK=PL, AB=AC => S(PAB)=S(PAC)

Sбп =S(PBC) +2S(PAB) =a^2/4 (cos(α/2) tgβ + ctg(α/2)/cosβ)

Приложения: