Математика, вопрос задал darktime11234 , 2 месяца назад

ТЕРМІНОВО даю 100 балів
Завдання на фото

Приложения:

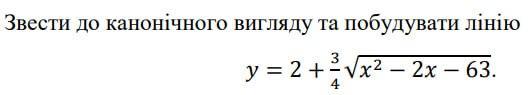
Ответы на вопрос

Ответил NNNLLL54

Ответ:

Привести уравнение к каноническому виду .

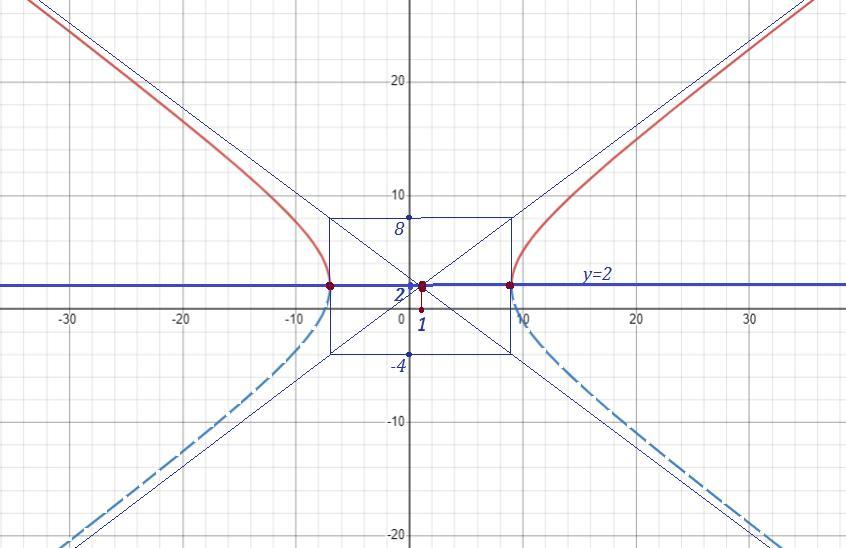
$\bf y=2+\dfrac{3}{4}\, \sqrt{x^2-2x-63}\\\\y-2=\dfrac{3}{4}\, \sqrt{x^2-2x-63}\ \ \ \Rightarrow\ \ \ y-2\geq 0\ \ ,\ \ y\geq 2\ \ ,\\\\y-2=\dfrac{3}{4}\, \sqrt{(x-1)^2-64}\\\\(y-2)^2=\dfrac{9}{16}\cdot \Big((x-1)^2-64\Big)\\\\(y-2)^2=\dfrac{9}{16}\cdot(x-1)^2-36\ \Big|\cdot 16\\\\9\cdot (x-1)^2-16\cdot (y-2)^2=36\cdot 16\\\\\dfrac{(x-1)^2}{64}-\dfrac{(y-2)^2}{36}=1$

Получили уравнение гиперболы , действительная полуось которой

а = 8 , мнимая полуось b = 6 , центр находится в точке ( 1 ; 2 ) .

Учитывая , что у ≥ 2 , делаем вывод , что исходное уравнение

задаёт половину гиперболы , расположенную над прямой у = 2 .

$\bf y=2+\dfrac{3}{4}\, \sqrt{x^2-2x-63}\ \ \ \ \Leftrightarrow \ \ \ \left\{\begin{array}{l}\bf y\geq 2\\\bf \dfrac{(x-1)^2}{64}-\dfrac{(y-2)^2}{36}=1\end{array}\right$