Геометрия, вопрос задал Bigmack228 , 6 лет назад

Теорема Пифагора.
Найлите: x

Приложения:

Ответы на вопрос

Ответил da2909

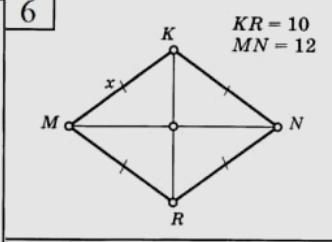
нам известно ,что у данного четырехугольника все сторны равны => по опрнделению это ромб

По свойтсву ромба диагонали при пересечению образуют перпендикуляр.

Значит, <KOM=<KON=<NOR=<MOR=90°

Также диагонали в точки пересечения лелятся пополам: KO=OR(5см) и MO=ON(6см)

Найдем стороны KM:

х найдем по теореме Пифагора.

с²=а²+b²

$c = \sqrt{a {}^{2} + b {}^{2} }$

a,b катеты

а=KO

b=MO

$c = \sqrt{5 {}^{2} + 6 {}^{2} }$

$c = \sqrt{61}$

Ответ :

$km = \sqrt{61}$

Bigmack228: спасибо за 1 задание, а как же 2?

Ответил ppp6491

Ответ: 1) Х =√61

2) х = 13

Объяснение: 1) Теорема Пифагора - квадрат гипотенузы равен сумме квадратов катетов.

В ромбе диагонали в точке пересечения делятся пополам. Таким образом Х² = (KR/2)² + (MN/2)². Отсюда Х = √{(KR/2)² + (MN/2)²} = √{(10/2)² + (12/2)²} = √(25+36) = √61

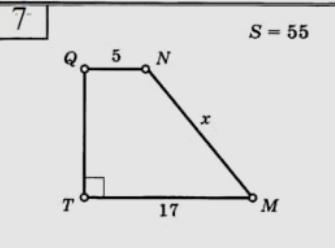
2) Площадь (S) трапеции равна произведению средней линии (Lср) трапеции на высоту (h) трапеции. Средняя линия трапеции равна половине суммы длин оснований, т.е. Lср = (QN + TM)/2 = (5 + 17)/2 =22/2 = 11. Теперь найдем высоту трапеции. h = S/Lср = 55/11 = 5.

См. рисунок. Из N опустим перпендикуляр на ТМ. Отсюда КМ = ТМ - КТ = 17 - 5 = 12 Тогда Х² = h² + КМ². Отсюда Х = √(h² + КМ²)= √(5²+ 12²) = √169 = 13

Приложения: