Тема: "Вычисление экстремумов функций нескольких переменных"
Задание: Найти стационарные точки функции двух переменных
Приложения:
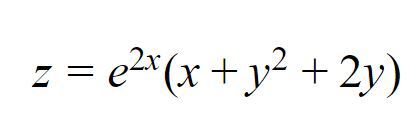
Ответы на вопрос
Ответил mefody66
0
Стационарные точки - это точки, в которых производные равны 0
z = e^(2x)*(x + y^2 + 2y)
{ dz/dx = 2e^(2x)*(x + y^2 + 2y) + e^(2x) = 0
{ dz/dy = e^(2x)*(2y + 2) = 0
Делим 1 уравнение на e^(2x), а 2 уравнение на 2e^(2x)
{ 2(x + y^2 + 2y) + 1 = 0
{ y + 1 = 0
Из 2 уравнения y = -1, подставляем в 1 уравнение
2(x + 1 - 2) + 1 = 2(x - 1) + 1 = 2x - 2 + 1 = 2x - 1 = 0
x = 1/2
z(1/2; -1) = e^1*(1/2 + 1 - 2) = e*(1/2 - 1) = -e/2
Ответ: (1/2; -1; -e/2)
z = e^(2x)*(x + y^2 + 2y)
{ dz/dx = 2e^(2x)*(x + y^2 + 2y) + e^(2x) = 0
{ dz/dy = e^(2x)*(2y + 2) = 0
Делим 1 уравнение на e^(2x), а 2 уравнение на 2e^(2x)
{ 2(x + y^2 + 2y) + 1 = 0
{ y + 1 = 0
Из 2 уравнения y = -1, подставляем в 1 уравнение
2(x + 1 - 2) + 1 = 2(x - 1) + 1 = 2x - 2 + 1 = 2x - 1 = 0
x = 1/2
z(1/2; -1) = e^1*(1/2 + 1 - 2) = e*(1/2 - 1) = -e/2
Ответ: (1/2; -1; -e/2)
Новые вопросы
Алгебра,
2 года назад
Русский язык,
2 года назад
Обществознание,
8 лет назад
Химия,
8 лет назад
Математика,
9 лет назад