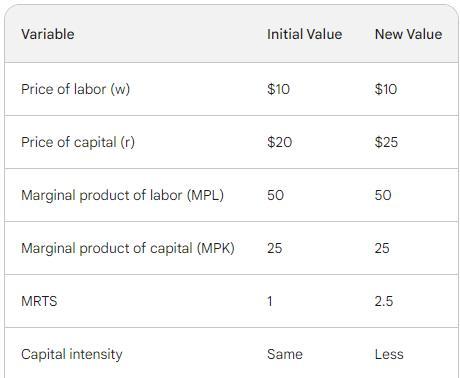
Suppose that the price of labor is $10 per unit and the price of capital is $20 per unit.

1. Assuming the firm is minimizing its cost, if the marginal product of labor is 50, what must the marginal product of capital be ?

2. Suppose the price of capital increases to $25 per unit, while the price of labor stays the same. To minimize the cost of producing the same level of output, would the firm become more capital-intensive or labor-intensive? Explain.

Assuming the firm is minimizing its cost, if the marginal product of labor is 50, the marginal product of capital must be 25. This can be found by setting the marginal rate of technical substitution (MRTS) equal to the ratio of the price of labor to the price of capital. The MRTS is defined as the change in capital divided by the change in labor that results in a constant level of output. In this case, the MRTS is equal to 1, since the firm is using one unit of labor for every unit of capital. Therefore, we have:

• MRTS = MPK / MPL = r / w

where:

• MPK is the marginal product of capital
• MPL is the marginal product of labor
• r is the price of capital
• w is the price of labor

Solving for MPK, we get:

• MPK = MPL * r / w = 50 * 20 / 10 = 25

2. Suppose the price of capital increases to $25 per unit, while the price of labor stays the same. To minimize the cost of producing the same level of output, the firm would become more labor-intensive. This can be seen by again setting the MRTS equal to the ratio of the price of labor to the price of capital. Now, the MRTS is equal to:

• MRTS = MPK / MPL = 25 / 10 = 2.5

• Since the MRTS is greater than 1, the firm will substitute away from capital and towards labor. This is because the relative price of capital has increased, making it less attractive relative to labor.

Here is a table summarizing the results: (photo).

As you can see, the firm's capital intensity decreases when the price of capital increases. This means that the firm will use less capital and more labor to produce the same level of output.