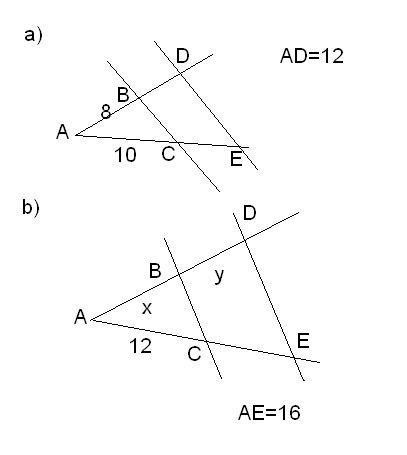
Стороны угла А пересечены двумя параллельными прямыми ВС и DE ( В и D на одной стороне угла) Найдите:
а) АЕ, если АВ=8 м, АD=12 м, АС = 10 м
б) АВ, если АВ+АD=21 м, АС=12 м, АЕ=16 м
90 БАЛЛОВ!
Ответы на вопрос
Ответил ssoxo
0
Тр-ки АВС и АДЕ подобны так как ∠АВС=∠АДЕ (ВС║ДЕ и АД - секущая), ∠А - общий.
а) АВ/АД=АС/АЕ ⇒ АЕ=АС·АД/АВ=10·12/8=15 м - это ответ.
б) Пусть АВ=х, тогда АД=21-х.
АВ/АД=АС/АЕ,
х/(21-х)=12/16,
16х=252-12х,
28х=252,
х=9.
АВ=9 м - это ответ.
а) АВ/АД=АС/АЕ ⇒ АЕ=АС·АД/АВ=10·12/8=15 м - это ответ.
б) Пусть АВ=х, тогда АД=21-х.
АВ/АД=АС/АЕ,
х/(21-х)=12/16,
16х=252-12х,
28х=252,
х=9.
АВ=9 м - это ответ.
Ответил marshal500
0
Решается по т. Фалеса. Параллельные прямые отсекают на сторонах угла пропорциональные отрезки.
а) АВ/AD=AC/AE;
8/12=10/AE;
AE=10*12/8=АЕ=15 м.
б) АВ-х, ВD-у, АD=х+у, АВ+АD=х+х+у=21 м, х+у=21-х;
(21-х)/х=16/12;
21/х=28/12;
х=21*12/28=АВ=9 м.
а) АВ/AD=AC/AE;
8/12=10/AE;
AE=10*12/8=АЕ=15 м.
б) АВ-х, ВD-у, АD=х+у, АВ+АD=х+х+у=21 м, х+у=21-х;
(21-х)/х=16/12;
21/х=28/12;
х=21*12/28=АВ=9 м.
Приложения:
Новые вопросы
Другие предметы,
2 года назад
Математика,
2 года назад
Химия,
8 лет назад
Математика,
8 лет назад
Математика,
9 лет назад
Биология,
9 лет назад