стороны треугольника равны 13 13 10 найдите радиус окружности проходящий через все его вершины​

Ответ:

R = 169/24 ≈ 7,04 см

Объяснение:

Окружность, проходящая через все вершины треугольника - это описанная окружность.

Радиус описанной окружности:

R = abc/(4S)

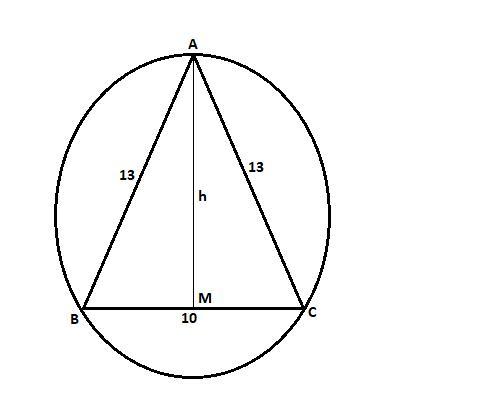
Смотрите рисунок.

В нашем случае треугольник ABC равнобедренный:

a = 10 см; b = c = 13 см.

Проведем высоту AM в треугольнике, она же медиана.

BM = CM = BC/2 = 10/2 = 5 см

Из теоремы Пифагора для прямоугольного треугольника ABM:

AM^2 + BM^2 = AB^2

AM^2 + 5^2 = 13^2

AM^2 = 169 - 25 = 144

AM = h = √144 = 12 см

S = a*h/2 = 10*12/2 = 120/2 = 60 кв.см.

R = abc/(4S) = 10*13*13/(4*60) = 1690/240 = 169/24 ≈ 7,04 см