стороны треугольника относятся как 3; 5; 7, а его периметр равен 60 см. Найдите периметр и стороны треугольника , вершины которого - середины сторон данного треугольника. (с рисунком и дано пожалуйста!!!!)))

Ответ:

Объяснение:

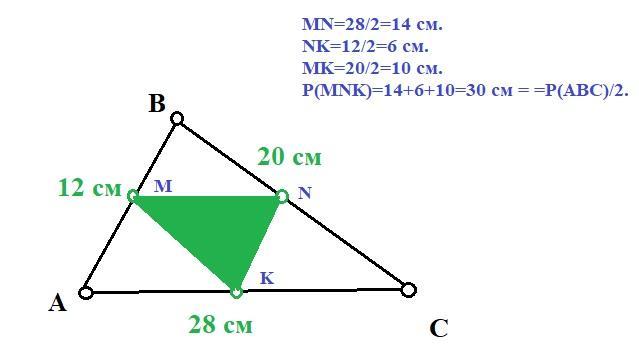
АВС- треугольник. АВ=3х.  ВС=5х.  АС=7х.  Периметр Р(АВС) = 60 см.

Р=3х+5х+7х=60.

15x=60.

x=4.

AB=3x=3*4=12 см.

ВС=5х=5*4=20 см.

АС=7х=7*4=28 см.

-----------------

Серединами сторон данного треугольника являются средние линии треугольника равные половине стороны ей параллельной.

Точки MN и K - середины сторон АВ,  ВС и АС, соответственно.

MN║AC,  MK║BC  и NK║AB/

MK=BC/2=20/2=10 см

MN=AC/2=28/2=14 см.

NK=AB/2=12/2=6 см.

---------------

Р(NMK)=6+10+14=30 см , то есть 1/2 от основного треугольника.