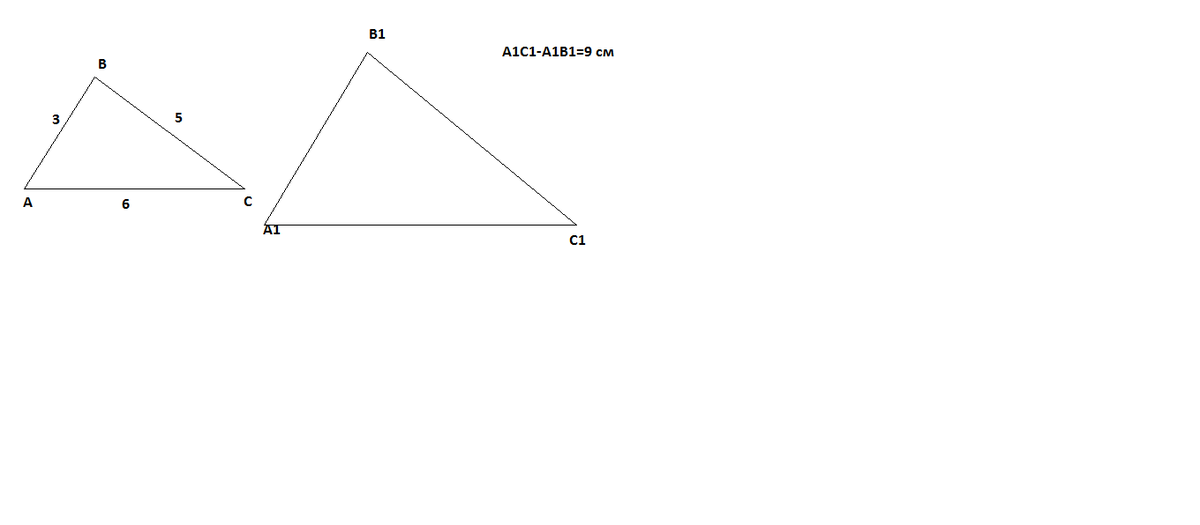
Стороны треугольника относятся как 3:5:6. Найдите стороны подобного ему треугольника, в котором разность наибольшей и наименьшей сторон равна 9 см.
Ответы на вопрос
Ответил Suasore
0
Поскольку треугольники подобны, то для А1В1С1 отношение сторон будет таким же: 3:5:6
А1В1 : В1С1 : А1С1 = 3 : 5 : 6
Зная разность сторон, запишем:
А1С1=9+А1В1.
А1В1 : А1С1 = 3 : 6
А1В1 : (9+А1В1)= 3 : 6
6А1В1 = 27 + 3А1В1
3А1В1=27
А1В1=9 см
Значит А1С1=9+9=18 см
Найдем неизвестную сторону В1С1:
А1В1 : В1С1 = 3 : 5
В1С1 = 9*5:3=15 см
А1В1 : В1С1 : А1С1 = 3 : 5 : 6
Зная разность сторон, запишем:
А1С1=9+А1В1.
А1В1 : А1С1 = 3 : 6
А1В1 : (9+А1В1)= 3 : 6
6А1В1 = 27 + 3А1В1
3А1В1=27
А1В1=9 см
Значит А1С1=9+9=18 см
Найдем неизвестную сторону В1С1:
А1В1 : В1С1 = 3 : 5
В1С1 = 9*5:3=15 см
Приложения:
Новые вопросы
Математика,
2 года назад
Литература,
2 года назад