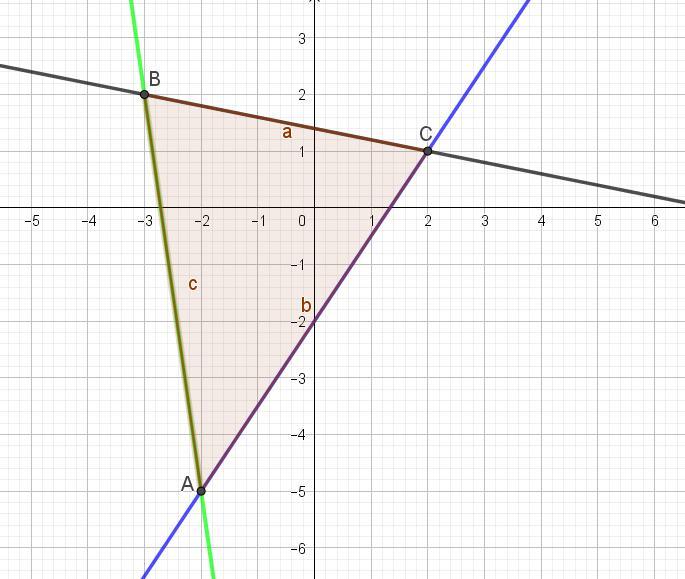
Стороны треугольника лежат на прямых x+5у–7=0, 3x–2y–4=0, 7x+y+19=0.
Вычислить его площадь S
Ответы на вопрос
Стороны треугольника лежат на прямых x+5у–7=0, 3x–2y–4=0, 7x+y+19=0. Вычислить его площадь S.
Находим координаты вершин треугольника как точки пересечения заданных прямых.
3x–2y–4=0, 3x–2y–4=0,
7x+y+19=0 |x2 = 14x+2y+38=0
17x + 34 = 0, x = -34/17 = -2.
y = (3/2)*x - (4/2) = y = (3/2)*(-2) - (4/2) = -3 - 2 = -5.
Точка А(-2; -5).
x+5у–7=0, |x-7 = -7x-35y+49=0
7x+y+19=0, 7x+y+19=0
-34y+68 = 0, y = -68/-34 = 2.
x = 7 - 5y = 7 - 5*2 = -3.
Точка В(-3; 2).
x+5у–7=0, |x(-3) = -3x-15y+21 = 0
3x–2y–4=0 3x–2y–4 = 0
-17y+17 = 0, y = -17/-17 = 1.
x = 7 - 5y = 7 - 5*1 = 2.
Точка С(2; 1).
Найдем вектора по координатам точек:
AB = {Bx - Ax; By - Ay; Bz - Az} = {-3 - (-2); 2 - (-5); 0 - 0} = {-1; 7; 0}
AC = {Cx - Ax; Cy - Ay; Cz - Az} = {2 - (-2); 1 - (-5); 0 - 0} = {4; 6; 0}
S = (1/2) |AB × AC|
Найдем векторное произведение векторов:
c = AB × AC
AB × AC =
i j k
ABx ABy ABz
ACx ACy ACz
=
i j k
-1 7 0
4 6 0
= i (7·0 - 0·6) - j ((-1)·0 - 0·4) + k ((-1)·6 - 7·4) =
= i (0 - 0) - j (0 - 0) + k (-6 - 28) = {0; 0; -34}
Найдем модуль вектора:
|c| = √(cx^2 + cy^2 + cz^2) = √(0^2 + 0^2 + (-34)^2) = √(0 + 0 + 1156) = √1156 = 34
Найдем площадь треугольника:
S = (1/2)* 34 = 17 .