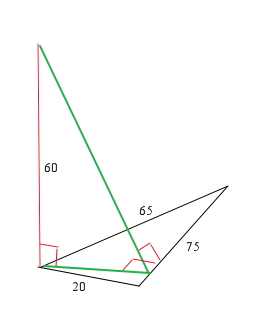
стороны треугольника 20 65 и 75 см. из вершины большего угла треугольника проведён к его плоскости перпендикуляр длиной 60 см. Найти расстояние от конца перпендикуляра до большей стороны треугольника
Ответы на вопрос
в треугольнике против бОльшей стороны лежит бОльший угол...
значит перпендикуляр проведен из угла, лежащего против стороны 75 см
искомое расстояние ---это перпендикуляр к стороне в 75 см, опущенный из конца перпендикуляра к плоскости треугольника
искомое расстояние ---это гипотенуза прямоугольного треугольника с катетом 60 см и вторым катетом---высотой данного треугольника, проведенной к стороне в 75 см
высоту исходного треугольника можно найти через его площадь...
по формуле Герона S = корень(p(p-a)(p-b)(p-c)), где р---полупериметр
S = корень(80*60*15*5) = корень(4*20*3*20*3*5*5) = 20*3*5*2 = 600
с другой стороны S = высота*75/2
высота*75/2 = 600
высота = 1200/75 = 16
по т.Пифагора искомое расстояние = корень(60*60+16*16) = корень(16*(15*15+16)) =
корень(16*241) = 4*корень(241)