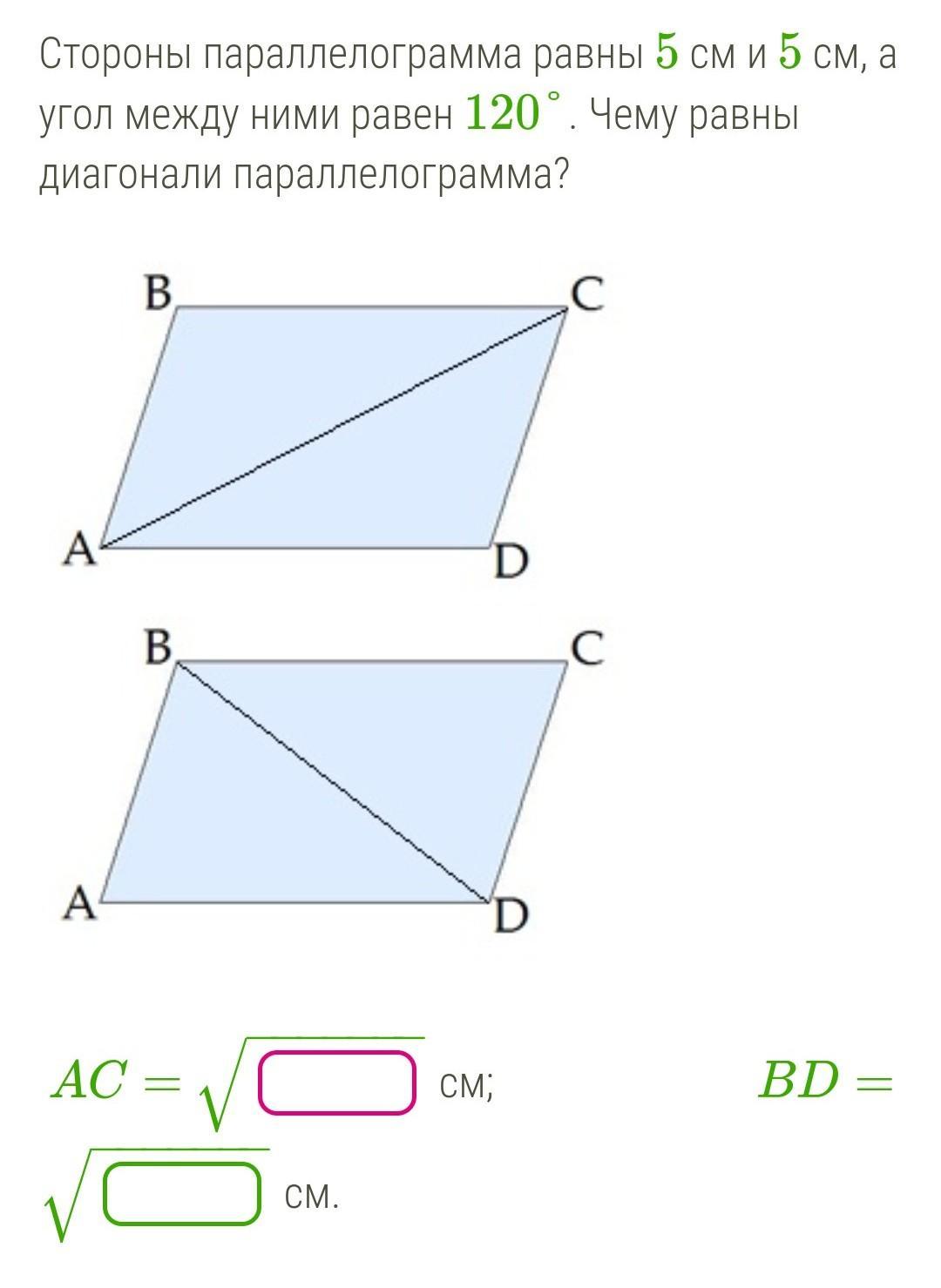
стороны параллелограмма равны 5 и 5см а угол между ними равен 120°. Чему равны диагонали параллелограмма?
АС=√
BE=√
Приложения:
Ответы на вопрос
Ответил orjabinina
1
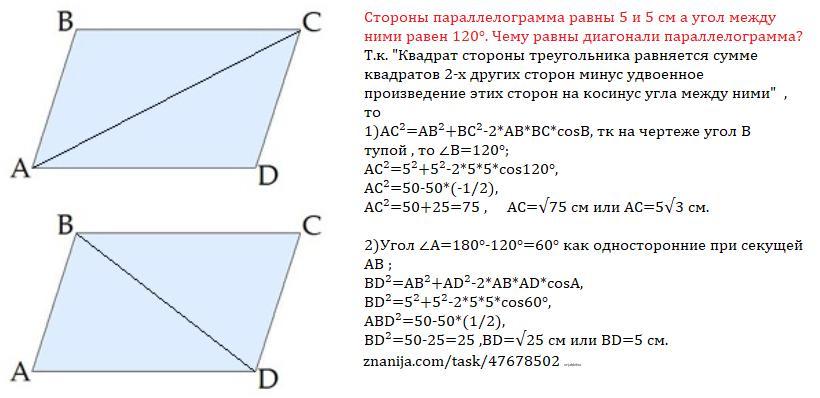
Стороны параллелограмма равны 5 и 5 см а угол между ними равен 120°. Чему равны диагонали параллелограмма?
Т.к. "Квадрат стороны треугольника равняется сумме квадратов 2-х других сторон минус удвоенное произведение этих сторон на косинус угла между ними" , то
1)АС²=АВ²+ВС²-2*АВ*ВС*cosВ, тк на чертеже угол В тупой , то ∠В=120°;
АС²=5²+5²-2*5*5*cos120°,
АС²=50-50*(-1/2),
АС²=50+25=75 , АС=√75 см или АС=5√3 см.
2)Угол ∠А=180°-120°=60° как односторонние при секущей АВ ;
BD²=АВ²+AD²-2*АВ*AD*cosA,
BD²=5²+5²-2*5*5*cos60°,
АBD²=50-50*(1/2),
BD²=50-25=25 ,BD=√25 см или BD=5 см.
Приложения:
anastasiamilickaa64:
под 1 там не может быть 5 корней из 3
там нужен просто корень
и во втором, там корень должен быть в ответе
BD=√25 , АС=√75 может так
хорошо
если не сложно можешь решить еще 1 задание по геометрии
Новые вопросы