стороны оснований правильной усеченной четырехугольной пирамиды равны 10 и 6 см а боковое ребро образует с плоскостью большего основания угол 45° найдите площадь диагонального сечения пирамиды
Ответы на вопрос
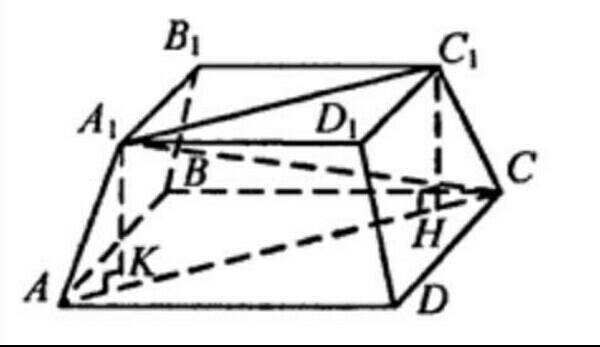
Обозначим данную правильную усечённую четырёхугольную пирамиду буквами ABCDA1B1C1D1.
∠A1AC = 45˚
AD = 6 см.
A1D1 = 10 см.
Диагональные сечение данной пирамиды - равнобедренная трапеция A1C1CA. (она равнобедренная, так как нам дана правильная пирамида)
Основания данной равнобедренной трапеции - A1C1 и АС.
Проведём диагонали A1C1 и AC.
S трапеции = (A1C1 + AC)/2 * высота трапеции.
Проведём в трапеции высоты A1K и С1Н. (они равны)
Так как данная пирамида - усечённая, правильная и четырёхугольная ⇒ основания данной пирамиды - квадраты.
Квадрат - геометрическая фигура, у которой все стороны равны.
⇒ АВ = ВС = CD = AD = 10 см, А1В1 = В1С1 = C1D1 = A1D1 = 6 см.
АС = АВ√2 = 10√2 см.
А1С1 = А1В1√2 = 6√2 см.
Теперь про высоты данной равнобедренной трапеции.
A1K = C1H = (AC - A1C1)/2 = ((10√2) - (6√2))/2 = 2√2 см.
△АА1К - прямоугольный, так как А1К - высота.
Сумма острых углов прямоугольного треугольника равна 90°.
⇒ ∠АА1К = 90° - ∠А1АС = 90° - 45° = 45°
Так как ∠АА1К = ∠А1АС = 45° ⇒ △А1АК - равнобедренный ⇒ А1К = АК = 2√2 см.
⇒ S трапеции А1С1СА = ((10√2) + (6√2))/2 * 2√2 = 32 см²
Ответ: 32 см²