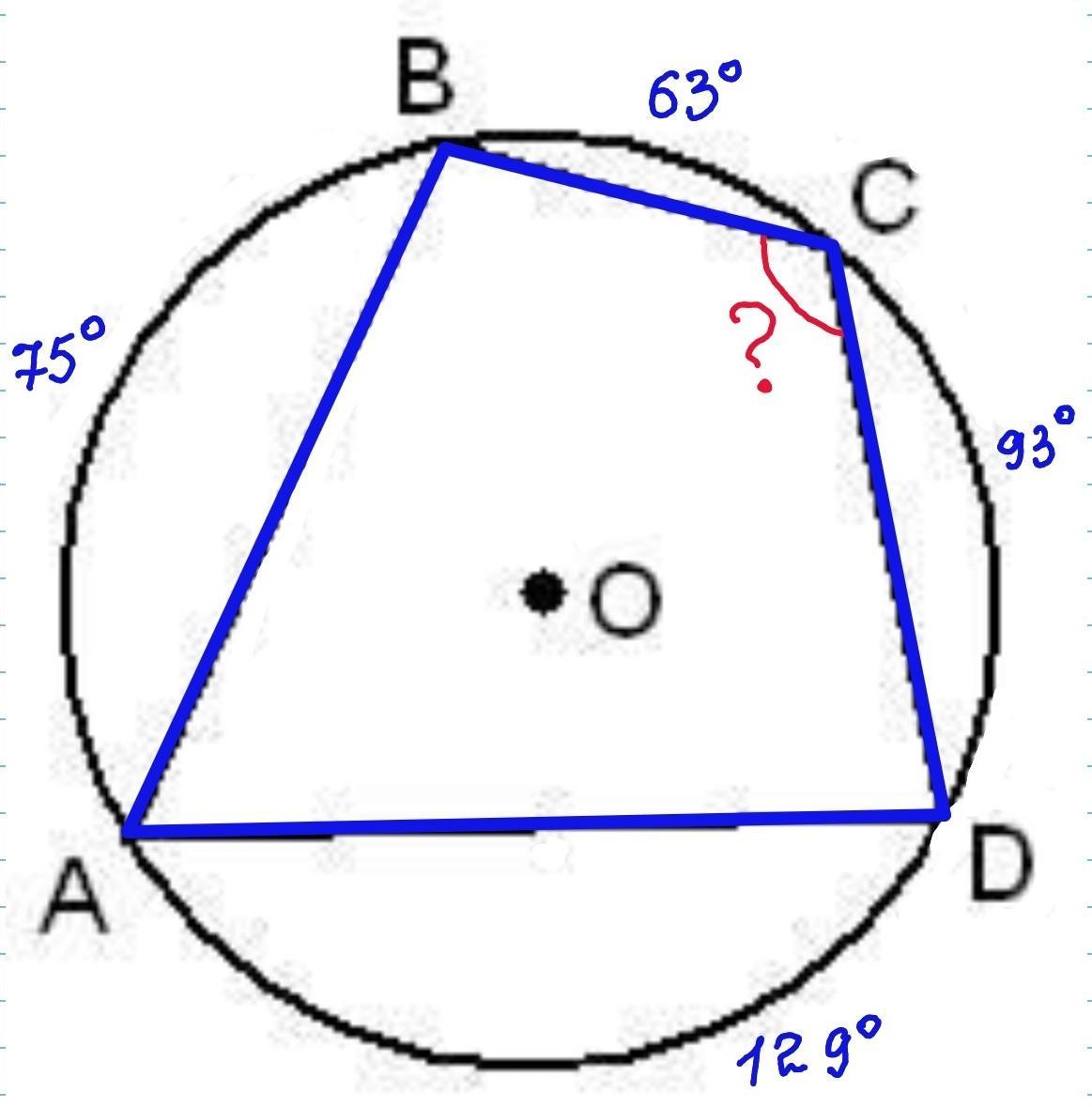
Стороны четырехугольника ABCD AB, BC, CD и AD стягивают дуги описанной окружности, градусные величины которых равны соответственно 75°, 63°, 93°, 129°. Найдите угол BCD этого четырехугольника. Ответ дайте в градусах.
Приложения:

Ответы на вопрос
Ответил ReMiDa
2
Стороны четырехугольника ABCD AB, BC, CD и AD стягивают дуги описанной окружности, градусные величины которых равны соответственно 75°, 63°, 93°, 129°. Найти угол BCD.
Ответ:
Угол BCD четырехугольника ABCD равен 102°.
Пошаговое объяснение:
∠BCD - вписанный угол.
- Вписанный угол равен половине градусной меры дуги, на которую он опирается.
∠BCD опирается на дугу BAD, которая равна сумме дуг AB и AD.
∠BCD = ½ • U BAD = ½ • (75°+129°) = 102°.
Приложения:
Новые вопросы