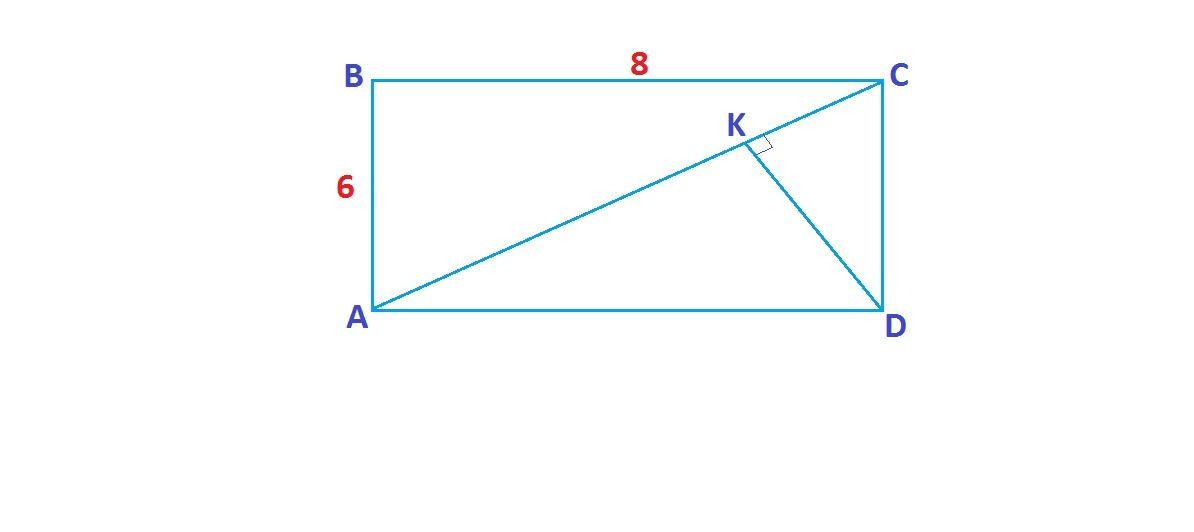
Геометрия, вопрос задал evgesha153 , 9 лет назад

Стороны ab и bc прямоугольника abcd равны 6 и 8 см.Найти длины отрезков на которые перпендикуляр,проведенный из вершины D к диагонали AC делит эту диагональ.

Ответы на вопрос

Ответил Luluput

$ABCD-$ прямоугольник
$AB=6$ см
$BC=8$ см
$AC-$ диагональ
$DK$ ⊥ $AC$
$AK-$ ?
$KC-$ ?

$ABCD-$ прямоугольник
$textless A= textless B= textless C= textless D=90к$
$AB=CD=6$ см
$BC=AD=8$ см
Δ $ABC-$ прямоугольный
по теореме Пифагора найдём AC:
$AC^2=AB^2+BC^2$
$AC^2=6^2+8^2$
$AC^2=100$
$AC=10$ см

$DK$ ⊥ $AC$
$AC=KC+AK$
$KC=x,$ $AK=10-x$
Воспользуемся теоремой о пропорциональных отрезках в прямоугольном треугольнике:
$b^2=b'*c$
$a^2=a'*c$
$a,b -$ катеты прямоугольного треугольника
$c-$ гипотенуза
$CD^2=CK*AC$
$6^2=x*10$
$10x=36$
$x=3.6$
$CK=3.6$ см
$AK=10-x$
$AK=10-3.6=6.4$ см

Ответ: 3.6 см; 6.4 см

Приложения:

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Математика, 6 лет назад

Будь-ласка допоможіть дуже срочн питання: Вкажіть число , протилежно числа 18...

Математика, 6 лет назад

У книжці 240 сторінок.Дівчинка прочитала 20% всієї книжки.Скільки сторінок прочитала дівчинка...

Геометрия, 9 лет назад

Сумма диагоналей ромба равна 70 см, а его периметр-100 см. Найдите диагонали ромба(только пожалуйста с полным объяснением)...

Физика, 9 лет назад

Температура тела A равна 300 K , температура тела Б равна 100 градусов по цельсию !Температура какого из тел повысится при тепловом контакте? 1) тела А 2) тела Б 3) температуры тел не...

Математика, 9 лет назад

сколько сантиметров в трех пятых метра?

География, 9 лет назад

Поставте по значению основные районы нефтедобычи : а)Волго-Уральский; б) Северный Кавказ; в) Среднее Приобье; г) Шельф побережья Баранцева моря. Как их значимость менялась за последние 50 лет?