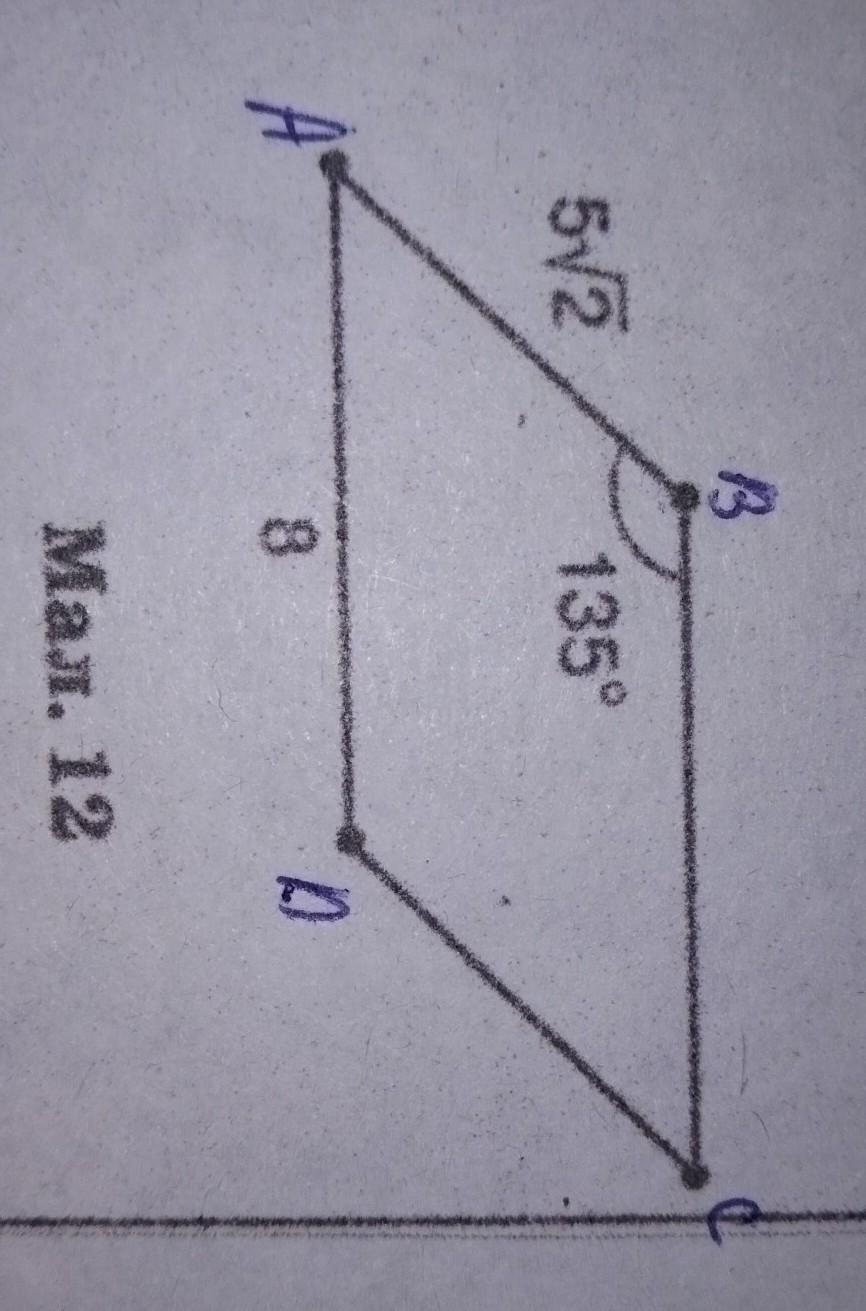
Сторони паралелограма дорівнюють AB=5√2 см і AD=8 см,кут В=135°.Знайдіть Довжину меншої діагоналі BD.
Розв'яжи задачу
Срочно даю 60 балов
Ответы на вопрос
Ответ:
У паралелограмі, коли ми знаємо сторони та один з кутів, можемо скористатися косинусним правилом для знаходження інших сторін та діагоналей.
За косинусним правилом в паралелограмі \( BD^2 = AB^2 + AD^2 - 2 \cdot AB \cdot AD \cdot \cos(B) \).
Для знаходження \( \cos(B) \) потрібно перевести кут \( 135^\circ \) в радіани, оскільки більшість тригонометричних функцій працюють з радіанами. \( 135^\circ = \frac{3\pi}{4} \) радіан.
Підставимо відомі значення:
\( BD^2 = (5\sqrt{2})^2 + 8^2 - 2 \cdot 5\sqrt{2} \cdot 8 \cdot \cos\left(\frac{3\pi}{4}\right) \).
Обчислимо це:
\( BD^2 = 50 + 64 - 80 \cdot \frac{-\sqrt{2}}{2} \).
\( BD^2 = 114 + 40\sqrt{2} \).
Отже, довжина меншої діагоналі \( BD = \sqrt{114 + 40\sqrt{2}} \approx 13.416 \) см (округлено до трьох знаків після коми).