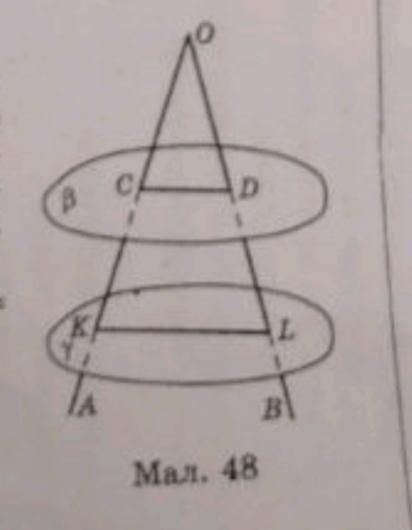
Сторони кута АОВ перетинають паралельні площини віу у точках С, D, K i L (мал. 48). ОС = 6 см, ОК = 12 см, KL = 8 см. Знайдіть CD.

Ответ:

З огляду на малюнок і інформацію, яка дана, ми маємо дві паралельні площини, які перетинають сторони кута \( \angle AOV \) в точках \( C \), \( D \), \( K \) і \( L \). Оскільки \( OK = 12 \) см і \( KL = 8 \) см, можемо визначити відстань між площинами, що проходить через ці точки, як \( KD = OK - KL = 12 - 8 = 4 \) см.

Тепер, оскільки \( CD \) є лінією, яка проходить паралельно площинам \( CK \) і \( DL \), \( CD \) також дорівнює \( KD \), оскільки вони є відстанями між паралельними площинами.

Отже, \( CD = KD = 4 \) см.

Объяснение:

надеюсь понятно