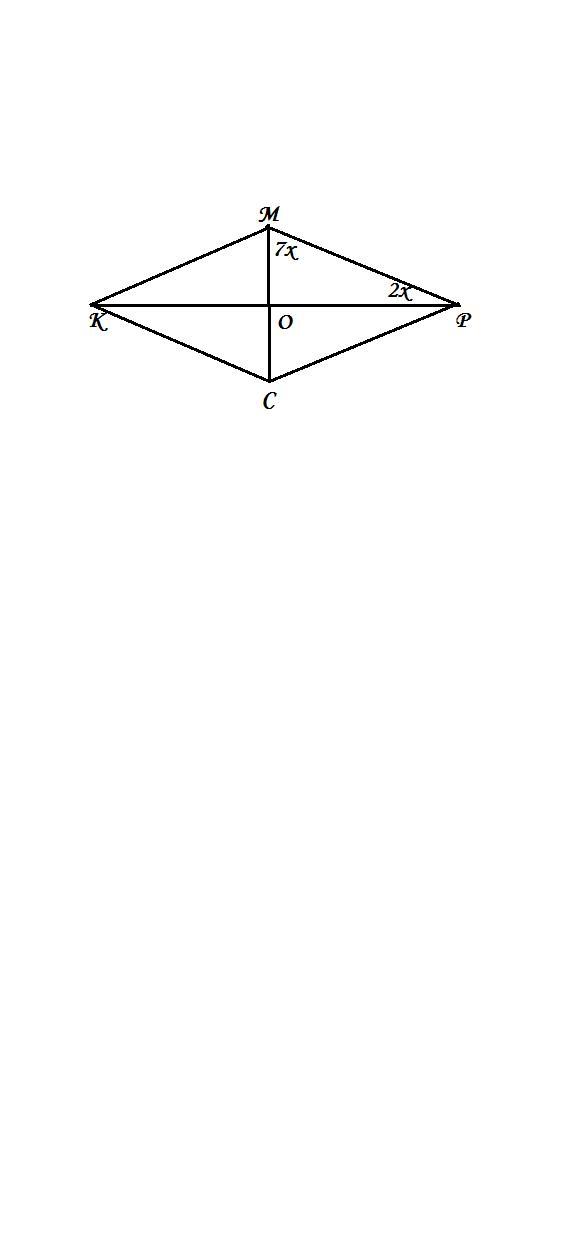
Сторона ромба утворює з його діагоналями кути, які відносяться як 2 : 7. Знайди кути ромба.
Ответы на вопрос
Нехай "a" - сторона ромба, "AC" і "BD" - його діагоналі. Кути, утворені діагоналями і сторонами ромба, є прягольниками, оскільки всі чотири кути ромба є прямими кутами.
За даними завдання, відомо, що відношення кутів між діагоналями і сторонами ромба дорівнює 2:7. Це означає, що:
1. Кут між "AC" і "a" дорівнює 2x.
2. Кут між "BD" і "a" дорівнює 7x.
У прямокутному прягольнику всі кути дорівнюють 90 градусів. Отже, сума всіх кутів у прягольнику повинна дорівнювати 360 градусів.
Оскільки у прягольнику є два кути "2x" і два кути "7x", ми можемо записати рівняння:
2x + 2x + 7x + 7x = 360
Згорнемо подібні доданки:
18x = 360
Тепер поділимо обидві сторони на 18, щоб знайти значення x:
x = 360 / 18
x = 20
Тепер ми знаємо значення x. Щоб знайти кути ромба, просто помножте x на відповідні коефіцієнти:
1. Кут між "AC" і "a" = 2x = 2 * 20 = 40 градусів.
2. Кут між "BD" і "a" = 7x = 7 * 20 = 140 градусів.
Отже, кути ромба дорівнюють 40 градусів і 140 градусів.
Ответ:
40° 140° 40° 140°
Объяснение:
Дано: СКМТ - ромб, КР і СМ - діагоналі, ∠МРО/∠РМО=2/7.
∠С, ∠К, ∠М, ∠Т - ?
Діагоналі ромба точкою перетину діляться навпіл, Діагоналі ромба перетинаються під прямим кутом.
ΔМОР - прямокутний; ∠МРО=2х°, ∠РМО=7х°
2х+7х=90; 9х=90; х=10.
∠МРО=20°, ∠РМО=70°
∠КМР=∠КСР=70*2=140°
∠МРС=∠МКС=20*2=40°