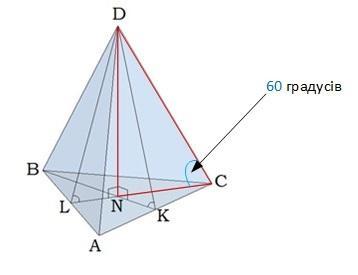
Математика, вопрос задал 14yulia27 , 1 год назад

Сторона основи правильної трикутної піраміди дорівнює 9 см, а бічне ребро утворює з площиною основи кут 60 градусів. Знайти висоту піраміди.

Ответы на вопрос

Ответил igorek1968igorek

Ответ:

9 см

Пошаговое объяснение:

АС = 9 см.

NC = $\frac{a*\sqrt{3} }{3}$ = $\frac{9*\sqrt{3} }{3}$

cos $60^{0}$ = $\frac{1}2}$

DC * cos $60^{0}$ = NC

DC * cos $60^{0}$ = $\frac{9*\sqrt{3} }{3}$

DC * $\frac{1}{2}$ = $\frac{9*\sqrt{3} }{3}$

DC = $\frac{9*\sqrt{3} }{3}$ ÷ $\frac{1}{2}$ = $\frac{9*\sqrt{3} }{3}$ * $\frac{2}{1}$ = $\frac{9*\sqrt{3} * 2 }{3}$

DC = $\frac{9*\sqrt{3} * 2 }{3}$

sin $60^{0}$ = $\frac{\sqrt{3} }{2}$

ND ÷ sin $60^{0}$ = DC

ND ÷ $\frac{\sqrt{3} }{2}$ = DC

ND = DC * $\frac{\sqrt{3} }{2}$

ND = $\frac{9*\sqrt{3} * 2 }{3}$ * $\frac{\sqrt{3} }{2}$ = $\frac{9*\sqrt{3} * 2 * \sqrt{3} }{3 * 2}$ = 9 см

ЯІкшо комусь потрібно, нижче пояснення рішення.

Піраміда, основою якої є правильний багатокутник, вершина якої проектується в центр основи, називається правильною пірамідою.

У нас основа піраміди трикутник, а точніше правильний трикутник.

Сторона основи правильного трикутника - це звичайна сторона трикутника, тільки у правильного трикутника всі сторони рівні, він рівносторонній трикутник.

Вияснили, шо у нас всі сторони трикутника при основі піраміди = 9 см

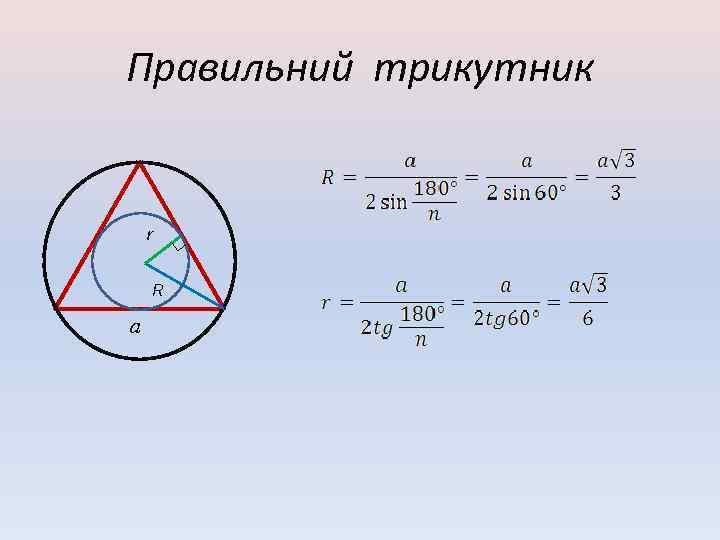
NC = $\frac{a*\sqrt{3} }{3}$ (на малюнку зліва подивись звідкіля я взяв цю формулу)

а - це у нас сторона трикутника при основі, тобто = 9 см.

NC = $\frac{a*\sqrt{3} }{3}$ = $\frac{9*\sqrt{3} }{3}$

Кут до бічної сторони = $60^{0}$ , це кут між гіпотенузою та прилеглою стороною. (гіпотенуза це найдовша сторона в прямокутному трикутнику, а остальні коротші сторони - то по научному називають катети).

В прямокутному трикутнику прилегла сторона (катет) в якесь число відрізняється від гіпотенузи, інакше кажучи якщо довжину катета помножити на шось, то віиде гіпотенуза.

Оте шось і є cos (косінус) ,

Катет в cos (косінус) раз відрізняється від гіпотенузи (довшої сторони).

Наш кут між цими сторонами = $60^{0}$

cos $60^{0}$ = $\frac{1}2}$

Тобто катет у нас відрізняється від гіпотенузи в $\frac{1}2}$ , або іншими словами гіпотенуза вдвічі довша від прилеглого катета.

А ми перед цим уже записали довжину цього прилеглого катету:

NC = $\frac{a*\sqrt{3} }{3}$ = $\frac{9*\sqrt{3} }{3}$

Довжина гіпотенузи вдвічі довша від нього:

DC * cos $60^{0}$ = NC

DC * cos $60^{0}$ = $\frac{9*\sqrt{3} }{3}$

DC * $\frac{1}{2}$ = $\frac{9*\sqrt{3} }{3}$

DC = $\frac{9*\sqrt{3} }{3}$ ÷ $\frac{1}{2}$ = $\frac{9*\sqrt{3} }{3}$ * $\frac{2}{1}$ = $\frac{9*\sqrt{3} * 2 }{3}$