Стационарный искусственный спутник Земли движется в плоскости экватора по круговой орбите так, что все время находится над одной и той же точкой земной поверхности. Определите орбитальную скорость спутника и высоту его орбиты над поверхностью Земли. Радиус Земли 6370 км.
Необходимо максимально подробное решение с сопроводительным рисунком.
Ответы на вопрос
Ответил WiLdToNnY
0
Хорошо понятое условие задачи, на половину решённая задача!
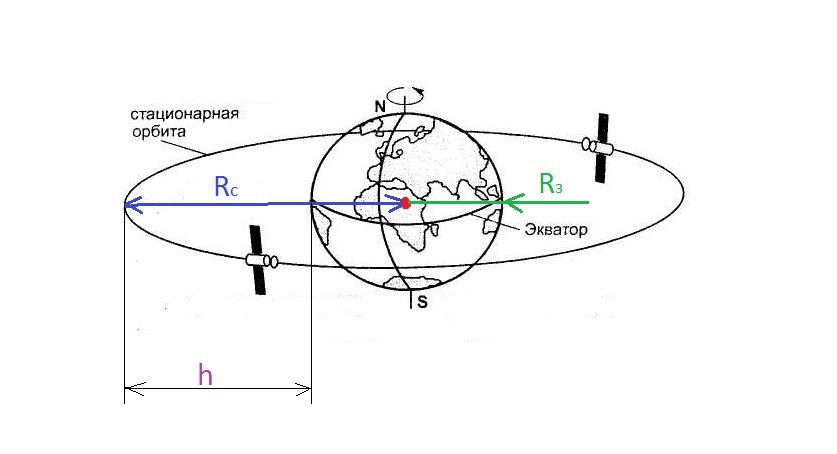
Начнём со слов: Стационарный искусственный спутник Земли, в плоскости экватора - думаю ясно что, спутник неподвижен относительно Земли и находится в точке над экватором.
Далее: Движется по круговой орбите так, что все время находится над одной и той же точкой земной поверхности - это означает что, линейная скорость вращения спутника по орбите, должна равна линейной скорости вращения Земли вокруг своей оси.
Определите орбитальную скорость спутника и высоту его орбиты над поверхностью Земли? Дальше математика:
Дано:

Найти:

Решение:
Запишем закон всемирного тяготения: относительно двух тел:
Спутник - Земля







![R_c= sqrt[3]{frac{T^2cdot Gcdot M}{4cdot pi^2} } = sqrt[3]{frac{86400^2cdot 6,67cdot10^{-11}cdot5,97cdot 10^{24}}{4cdot 3,14^2}} = 42241187,7 (_M) R_c= sqrt[3]{frac{T^2cdot Gcdot M}{4cdot pi^2} } = sqrt[3]{frac{86400^2cdot 6,67cdot10^{-11}cdot5,97cdot 10^{24}}{4cdot 3,14^2}} = 42241187,7 (_M)](https://tex.z-dn.net/?f=R_c%3D+sqrt%5B3%5D%7Bfrac%7BT%5E2cdot+Gcdot+M%7D%7B4cdot+pi%5E2%7D+%7D+%3D+sqrt%5B3%5D%7Bfrac%7B86400%5E2cdot+6%2C67cdot10%5E%7B-11%7Dcdot5%2C97cdot+10%5E%7B24%7D%7D%7B4cdot+3%2C14%5E2%7D%7D+%3D+42241187%2C7++%28_M%29)
Это всё определяли радиус орбиты по которой движется спутник. Сейчас определяем его скорость:

Высота на которой находится спутник от Земли:

Начнём со слов: Стационарный искусственный спутник Земли, в плоскости экватора - думаю ясно что, спутник неподвижен относительно Земли и находится в точке над экватором.
Далее: Движется по круговой орбите так, что все время находится над одной и той же точкой земной поверхности - это означает что, линейная скорость вращения спутника по орбите, должна равна линейной скорости вращения Земли вокруг своей оси.
Определите орбитальную скорость спутника и высоту его орбиты над поверхностью Земли? Дальше математика:
Дано:
Найти:
Решение:
Запишем закон всемирного тяготения: относительно двух тел:
Спутник - Земля
Это всё определяли радиус орбиты по которой движется спутник. Сейчас определяем его скорость:
Высота на которой находится спутник от Земли:
Приложения:
Новые вопросы
Биология,
2 года назад
Математика,
8 лет назад
Математика,
8 лет назад
Математика,
9 лет назад
История,
9 лет назад