срочнооо помогите пожалуйста умоляю напишите задачу с *АНАЛИЗОМ* ппожалуйста с условием. пожалуйста
Ответы на вопрос
Ответ:
Катеты равны 8 см и 15 см.
Объяснение:
Пусть a и b -- катеты прямоугольного треугольника. Тогда по условию:
a + b = 23
ab / 2 = 60
Выразим b через a из первого уравнения: b = 23 – a. Подставим получившееся значение во второе уравнение:
a(23 – a) / 2 = 60
a(23 – a) = 120
23a – a² = 120
a² – 23a + 120 = 0
D = 23² – 4·120 = 49 = 7²
a₁ = (23 – 7) / 2 = 8 ⇒ b₁ = 23 – 8 = 15
a₂ = (23 + 7) / 2 = 15 ⇒ b₂ = 23 – 15 = 8
Полученные решения совпадают с точностью до перестановки катетов местами.
Ответ:
8см, 15см
Объяснение:
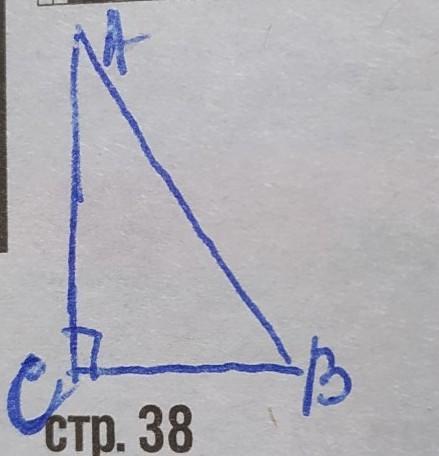
пусть катет АС=х, а катет ВС=23–х.
Поскольку площадь треугольника 60см², то она вычисляется по формуле:
тогда:
23x–x²=120
–x²+23x–120=0 |×(–1)
x²–23x+120=0
D= b²–4×ac=23²–4×1×120=529–480=49
Тогда АС1=15см, или АС2=8см,
ВС1=23–15=8см
ВС2=23–8=15см
Итак: катеты в треугольнике составляют 8см и 15см