Геометрия, вопрос задал Madsee , 2 года назад

Срочно Вокруг цилиндра описана правильная треугольная призма. Найти объем призмы если обьем цилиндра равен 2п√3

Ответы на вопрос

Ответил KuOV

Ответ:

18 куб. ед.

Объяснение:

Объем цилиндра:

Vц. = πR²h

Vц. = 2π√3

πr²h = 2π√3

r²h = 2√3 (1)

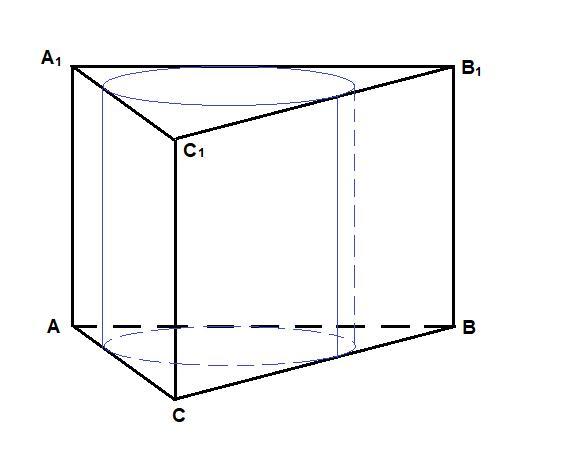
Призма описана около цилиндра, значит высота призмы равна высоте цилиндра, а радиус цилиндра равен радиусу окружности, вписанной в основание призмы.

Призма правильная, значит ΔАВС - правильный.

Радиус окружности, вписанной в правильный треугольник со стороной а:

$r=\dfrac{a\sqrt{3}}{6}$

$a=\dfrac{6r}{\sqrt{3}}=\dfrac{6r\sqrt{3}}{3}=2r\sqrt{3}$

Площадь правильного треугольника со стороной а:

$S=\dfrac{a^2\sqrt{3}}{4}$

$S=\dfrac{(2r\sqrt{3})^2\sqrt{3}}{4}=\dfrac{4r^2\cdot 3\cdot \sqrt{3}}{4}=3r^2\sqrt{3}$

Объем призмы равен произведению площади основания на высоту:

V = Sh

$V=3r^2\sqrt{3}\cdot h=3\sqrt{3}r^2h$

Учитывая равенство (1), получаем:

$V=3\sqrt{3}\cdot 2\sqrt{3}=6\cdot 3=18$

Приложения:

Новые вопросы

Русский язык, 1 год назад

Русский язык, 1 год назад

Химия, 2 года назад

Алгебра, 2 года назад

Математика, 7 лет назад

Обществознание, 7 лет назад