СРОЧНО

 

В треугольнике АВС известно, что АВ = 18, ВС = 16, cos∠В=4/9, АН – высота. Через точку Н проведена прямая, отсекающая от треугольника подобный ему треугольник и пересекающая сторну АВ в точке М. Найдите НМ.

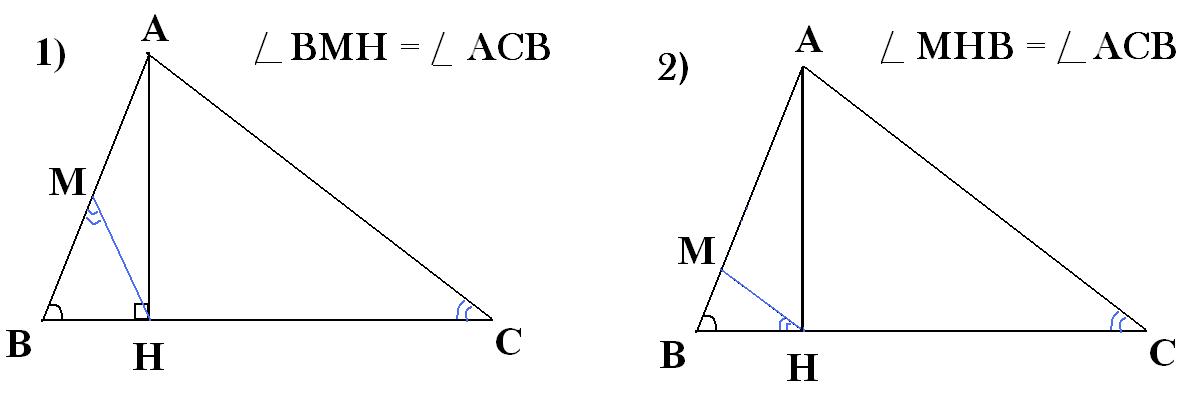
Чертежи к задаче - во вложении.

По условию задачи в силу подобия треугольников АВС и ВМН необходимо рассмотреть 2 случая.

1-й случай.

Из подобия треугольников следует равенство ∠АВС=∠MBH (по условию) и ∠АСВ=∠ВMН.

Тогда отношение сходственных сторон:

По теореме косинусов в ∆АВС АС²=АВ²+ВС²-2·АВ·ВС·cos B=18²+16²-2·18·16·4/9=18²+16²-16²=18²   => AC=18

В прямоугольном ∆АНВ   ВН=АВcosB= 18·4/9=8

Тогда получим

2-й случай.

Из подобия треугольников следует равенство ∠АВС=∠MBH (по условию)  и ∠АСВ=∠MНB.

Тогда MH||AC и отношение сходственных сторон:

Ответ: 8 или 9.