Математика, вопрос задал gromnata35 , 6 лет назад

срочно сегодня здавать с обьяснением пожалуйста даю 30баллов

Приложения:

Ответы на вопрос

Ответил ostashovdenisk

Ответ:

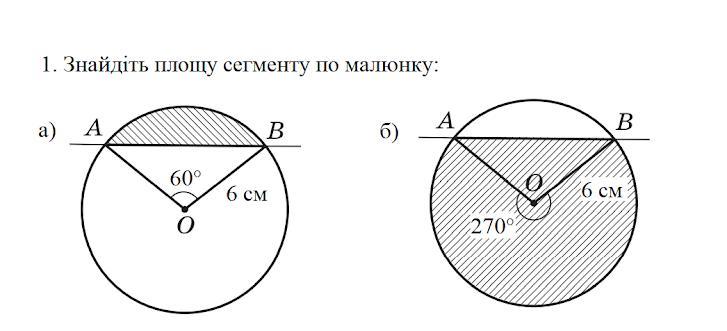
a)6π - 9√3 см^2

b)27π+18 см^2

Пошаговое объяснение:

a) $\alpha=60^\circ, r=6\; cm$

Пусть $S_{cek}$ - площадь сектора, не содержащего закрашенную фигуру,

S - площадь закрашенной фигуры, $S_\circ$ - площадь круга. Тогда $S = S_\circ -S_{\triangle AOB}-S_{cek}$

Площадь треугольника равна половине произведения двух его сторон на синус угла между ними, значит $S_{\triangle AOB}=\frac{1}{2}\cdot r^2\cdot \sin(\alpha)=\frac{1}{2}\cdot (6\; cm)^2\cdot \sin(60^\circ)=\frac{1}{2}\cdot 36\; cm^2\cdot \frac{\sqrt3}{2}=9\sqrt3\; cm^2$

$S_{cek}=\frac{\pi\cdot r^2\cdot (360^\circ-\alpha)}{360^\circ}=\frac{\pi\cdot (6\; cm)^2\cdot (360^\circ-60^\circ)}{360^\circ}=36\pi\; cm^2\cdot \frac{5}{6}=30\pi\; cm^2$

$S_\circ=\pi\cdot r^2=36\pi\; cm^2$

$S = S_\circ -S_{\triangle AOB}-S_{cek}=36\pi\; cm^2-9\sqrt3\; cm^2 -30\pi\; cm^2=6\pi-9\sqrt3\; cm^2$

b) $\alpha=270^\circ, r=6\; cm$

Пусть S - площадь закрашенной фигуры, $S_{cek}$ - площадь сектора внутри закрашенной фигуры, не содержащего $\triangle AOB$ . Тогда $S = S_{\triangle AOB}+S_{cek}$

$S_{cek}=\frac{\pi\cdot r^2\cdot \alpha}{360^\circ}=\frac{\pi\cdot (6\; cm)^2\cdot 270^\circ}{360^\circ}=36\pi\; cm^2\cdot \frac{3}{4}=27\pi\; cm^2$

$S_{\triangle AOB}=\frac{1}{2}\cdot r^2\cdot \sin(360^\circ-\alpha)=\frac{1}{2}\cdot (6\; cm)^2\cdot \sin(360^\circ - 270^\circ)=\frac{1}{2}\cdot 36\; cm^2\cdot \sin(90^\circ)=18\; cm^2$

$S = S_{\triangle AOB}+S_{cek}=18\; cm^2+27\pi\; cm^2$

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Русский язык, 1 год назад

родственные слова к сеновалу...

Русский язык, 1 год назад

Срочно, пожалуйста. Под цифрой 3 Выписать словосочетания с числительными , поставить их в Т.п и П.п Творительный и предложные падежи...

Математика, 6 лет назад

Знайди два числа, якщо відомо, що їх сума дорівнює 34, а різниця 18. Першим записуй більше число, Відповідь: числа |...

Математика, 6 лет назад

100,26:9 розв‘язати в стопчик...

Алгебра, 8 лет назад

если sinx+cosx=0,8 то как найти sin^3 x+cos^3 x=?

Математика, 8 лет назад

Раскройте скобки и найдите значение выражения -0,23+(5,3-6,77) 8 17/39 - ( 7 1/2 - 4 22/39) И - 19,47 - ( - 20,69 - 3,32)...