Алгебра, вопрос задал masterjkds , 1 год назад

СРОЧНО РЕШИТЕ ПОЖАЛУЙСТА, ОЧЕНЬ СРОЧНО НУЖНО

Приложения:

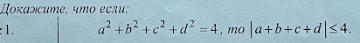
Ответы на вопрос

Ответил MrSolution

Ответ:

(см. объяснение)

Объяснение:

Рассмотрим сначала запись $a^2+b^2+c^2+d^2=4$ .

Поделим обе части равенства на 4 и извлечем из этих обеих частей квадратный корень (каждая часть равенства неотрицательна):

$\sqrt{\dfrac{a^2+b^2+c^2+d^2}{4}}=1$

Теперь перейдем к оценке:

$\dfrac{1}{4}\left|a+b+c+d\right|\le\dfrac{|a|+|b|+|c|+|d|}{4}\le\sqrt{\dfrac{a^2+b^2+c^2+d^2}{4}}=1$

При оценке были применены факты того, что модуль суммы не превосходит сумму модулей, неравенство о средних и выше замеченный факт (с равенством корня одному)

То есть было показано, что:

$\dfrac{1}{4}|a+b+c+d|\le1$