Алгебра, вопрос задал jackson0501 , 1 год назад

Срочно!!!решите логарифмическое уравнение(подробно)

Приложения:

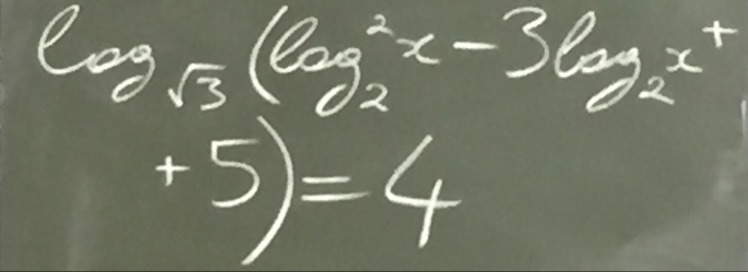
jackson0501: Уже сам решил

jackson0501: Спасибо

Ответы на вопрос

Ответил skvrttt

$log_{\sqrt{3}}(log_2^2x-3log_2x+5)=4\\log_2^2x-3log_2x+5=(\sqrt{3})^4\\log_2^2x-3log_2x-4=0\to\left[\begin{array}{ccc}log_2x_1=-1\\log_2x_2=4\end{array}\right\to\left[\begin{array}{ccc}x_1=\frac{1}{2}\\x_2=16\end{array}\right$

ОДЗ: $\left[\begin{array}{ccc}log_2^2x-3log_2x+5\ \textgreater \ 0\\x\ \textgreater \ 0\end{array}\right$

дискриминант квадратного трёхчлена $log_2^2x-3log_2x+5$ отрицательный, следовательно, само значение квадратного трёхчлена всегда положительно, а отсюда уже следует, что любое значение переменной икс (большее нуля, конечно) удовлетворяет нас, и что неравенство получается верное. Итак, одз: $x\ \textgreater \ 0$

jackson0501: Я уже решил

jackson0501: И у тебя неправильно

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Алгебра, 1 год назад

Помогите пожалуйста решить 8 класс...

Русский язык, 1 год назад

Задание: Выпишите существительные, которые без не не употребляются. (Не)годование, (не)видимка, (не)внимательность, (не)вежа, (не)вежда, (не)грамотность, (не)доверие, (не)забудка.

Математика, 1 год назад

В Треугольнике PRS Ps =55 мм, PS>PR в 2 раза. Чему равны стороны PS и PR, если периметр= 125 мм.( 5 класс)...

Математика, 1 год назад

Помогите решить 4 задание...

Алгебра, 7 лет назад

Помогите пожалуйста ...

История, 7 лет назад

Какое значение имело принятие Декларации прав человека и гражданина 1789 по мнению русских историков?