Математика, вопрос задал Аноним , 7 лет назад

СРОЧНО развязать интеграл(интегрування дифференцированням бинома) ОТ РУКИ НА ЛИСТКЕ​

Приложения:

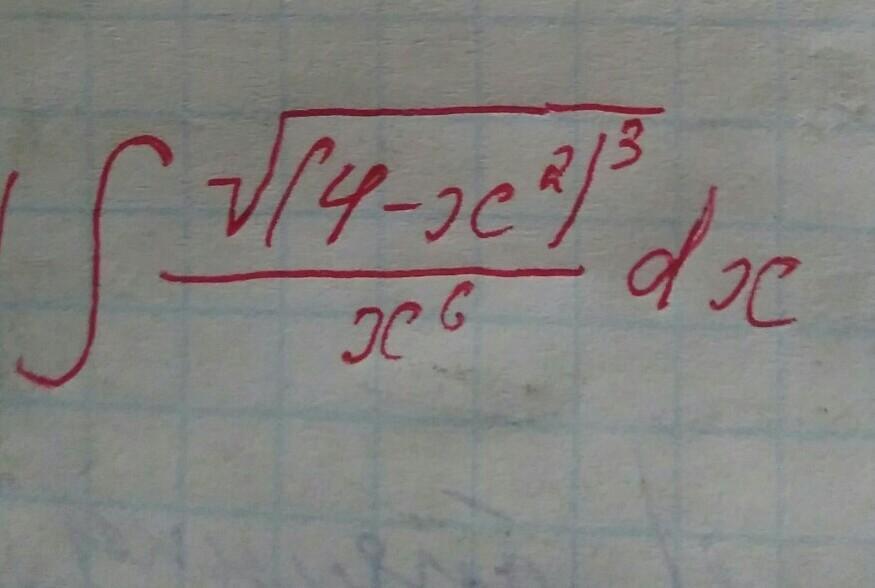
Ответы на вопрос

Ответил NNNLLL54
0

int frac{sqrt{(4-x^2)^3}}{x^6}, dx=[; x=2sint; , dx=2, cost, dt; ,\\4-x^2=4-4sin^2t=4(1-sin^2t)=4cos^2t; ]=int frac{sqrt{4cos^2t}cdot 2, cost, dt}{2^6cdot sin^6t}=\\=frac{1}{2^4}int frac{cos^2t, dt}{sin^6t}=frac{1}{16}int ctg^2tcdot frac{1}{sin^2t}cdot frac{dt}{sin^2t}=\\=frac{1}{16}int ctg^2tcdot (1+ctg^2t)cdot (-d(ctgt))=-frac{1}{16}int (ctg^2t+ctg^4t)cdot d(ctgt)=

=-frac{1}{16}cdot (frac{ctg^3t}{3}+frac{ctg^5t}{5})+C=-frac{1}{16}cdot Big (frac{1}{3}ctg^3(arcsinfrac{x}{2})+frac{1}{5}, ctg^5(arcsinfrac{x}{2})Big )+C=\\=-frac{1}{48}, Big (frac{sqrt{4-x^2}}{x}Big )^3-frac{1}{80}, Big (frac{sqrt{4-x^2}}{x}Big )^5+C=\\=-frac{sqrt{(4-x^2)^3}}{48x^3}-frac{sqrt{(4-x^2)^5}}{80x^5}+C

Предыдущий вопрос
Следующий вопрос
Новые вопросы
Английский язык, 1 год назад
5 предложений   в буд, вр,  , помогите ...
Русский язык, 1 год назад
Синтаксический разбор:Герасим поглядел на несчастную собачку, подхватил её одной рукой.
Математика, 7 лет назад
Оля собрала 8 Горшков для растений из деталей конструктора 1 горшок состоял из 16 деталей она каждый следующий потребовалось детали на 5 больше чем на предыдущей с помощью текста задачи Ответь на...
Математика, 7 лет назад
Помогите пожалуйста решить пример 4010-106*150:300= Помогите...
География, 8 лет назад
возраст тектонической структуре кавказ...
Математика, 8 лет назад
дам много баллов если поможете решить все по действиям...