СРОЧНО ПОЖАЛУЙСТА!!!!!!!!!!

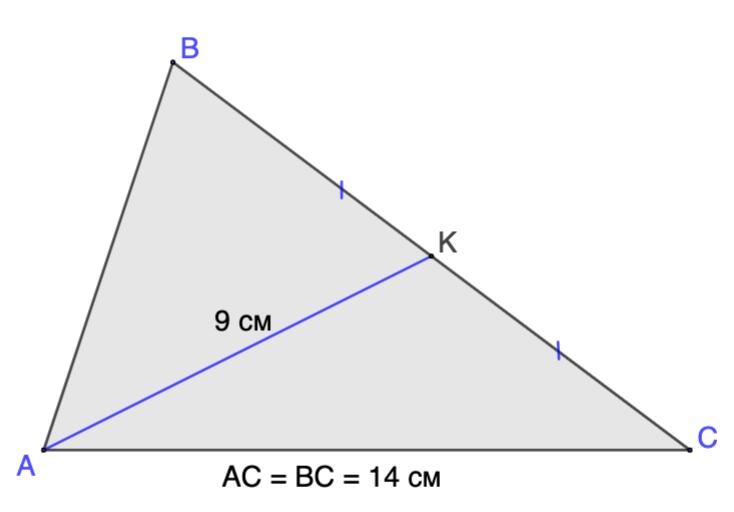
В треугольнике ABC проведена медиана AK , равна

9 см. Известно, что BC = AC = 14 см. Найдите площадь

треугольника ABC.

Ответ:

Площадь треугольника АВС равна 24√5 см².

Объяснение:

В треугольнике ABC проведена медиана AK , равна 9 см. Известно, что BC = AC = 14 см. Найдите площадь треугольника ABС.

Дано: ΔАВС - равнобедренный;

BC = AC = 14 см;

АК = 9 см - медиана.

Найти: S(ABC)

Решение:

Рассмотрим ΔАКС.

АК = 9 см; АС = 14 см (условие)

КС = ВС : 2 = 7 (см) (АК - медиана)

• Найдем площадь по формуле Герона:

                 ,

где р - полупериметр; а, b и с - стороны треугольника.

р = (9 + 14 + 7) : 2 = 15 (см)

• Медиана делит треугольник на два равновеликих треугольника.

⇒ S(AKC) = S(ABK) = 12√5 cм²

S(ABC) = S(AKC) + S(ABK) = 24√5 cм².

#SPJ1